Analyse de la covariance

class: center, middle, inverse, title-slide

# Analyse de la covariance
### Marie-Pierre Etienne
### <a href="mailto:marie-pierre.etienne@agrocampus-ouest.fr" class="email">marie-pierre.etienne@agrocampus-ouest.fr</a>
### 2021/11/19 (updated: 2023-09-08)

---

---
name: ancova
# Comparaison de droite de régression : modèle d'analyse de la covariance

--
## Cadre général
C'est la situation où 
* la variable à expliquer `$Y$` est quantitative
* Les variables explicatives sont qualitatives et quantitatives

```
## `geom_smooth()` using formula 'y ~ x'
```

```
## Warning: Removed 2 rows containing non-finite values (stat_smooth).
```

```
## Warning: Removed 2 rows containing missing values (geom_point).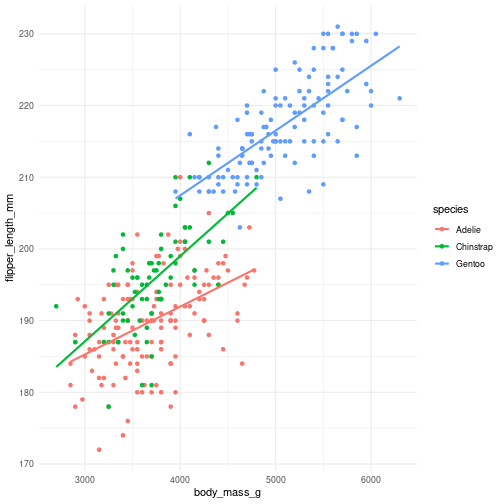
```

![](ancova_files/figure-html/load_penguins-1.png)

---

template: ancova
## Le modèle

`$$M_{comp} : \class{alea}{Y_{ik}} = \class{rouge}{\mu} + \class{rouge}{\alpha_i} + \class{rouge}{\beta}x_{ik} +\class{rouge}{\gamma_i} x_{ik} + \class{alea}{E_{ik}},\quad \class{alea}{E_{ik}}\overset{ind}{\sim}\mathcal{N}(0, \class{rouge}{\sigma^2}),$$`
avec 
- `$i=1,\ldots,I$` le niveau du facteur 1,
- `$x_{ik}$` la mesure de la variable quantitative `$x$` sur l'individu `$k$` du groupe `$i$`, 
- `$\class{rouge}{\mu}$` l'ordonnée à l'origine de référence,
- `$\class{rouge}{\alpha_i}$` l'effet différentiel de l'espèce `$i$` sur l'ordonnée à l'origine, ( `$\alpha_1=0$` )
- `$\class{rouge}{\beta}$` l'effet de la variable `$x$` pour le groupe de référence,   
- `$\class{rouge}{\gamma_i}$` l'effet différentiel de la variable `$x$` pour le groupe `$i$` par rapport au groupe de référence ( `$\gamma_1=0$` ),  
- `$\class{rouge}{\sigma^2}$` la variance commune à tous les groupes.

### Nombre de paramètres du modèle

- `$2I$` paramètres de moyenne  `$(\class{rouge}{(\mu, \alpha_2, \ldots, \alpha_I, \beta, \gamma_2, \ldots, \gamma_I)}$`; 
- 1 paramètre de variance `$\class{rouge}{\sigma^2}$`

---
name: test_complet

# Tests dans le modèle d'analyse de la covariance

--
## Test du modèle complet

Pour répondre à la question "La longueur des ailes des manchots est elle liée à leur masse et/ou à leur espèce ?"

`$$\begin{align} 
H_0 & =\left \lbrace \mbox{La longueur des ailes est la même en moyenne quelque soit la masse ou l'espèce du manchot }\right\rbrace\\
    & =\left \lbrace  \mbox{pour tout }i, \alpha_i =0,  \gamma_i = 0 \mbox{ et }\beta=0   \right\rbrace\\
    & =\left \lbrace  M_{comp} \mbox{ est équivalent à } M0 \right\rbrace.
\end{align}$$`

`$H_1$` prend les formes équivalentes suivantes

`$$\begin{align} 
H_1 & =\left \lbrace \mbox{la longueur des ailes varie selon la masse ou l'espèce }\right\rbrace\\
    & =\left \lbrace  \mbox{Il existe un }i, \alpha_i  \ne 0  \mbox{ ou un } \gamma_i \ne 0  \mbox{ ou } \beta \ne 0 \right\rbrace\\
    & =\left \lbrace  M_{comp} \mbox{ est préférable à } M0 \right\rbrace.
\end{align}$$`
---
template: test_complet

## Test du modèle complet

### Statistique de test

$$ F = \frac{\frac{RSS_0-RSS}{2I-1}}{\frac{RSS}{n-2I}} \underset{H_0}{\sim} \mathcal{F}(2I-1, n-2I) $$
---
template: test_complet

## Test du modèle complet sur l'exemple manchot

```r
Mcomp <- lm(flipper_length_mm ~ species + body_mass_g + species:body_mass_g, data =penguins)
M0 <- lm(flipper_length_mm ~ 1, data =penguins)
anova(M0, Mcomp)
```

```
## Analysis of Variance Table
## 
## Model 1: flipper_length_mm ~ 1
## Model 2: flipper_length_mm ~ species + body_mass_g + species:body_mass_g
##   Res.Df   RSS Df Sum of Sq      F    Pr(>F)    
## 1    341 67427                                  
## 2    336  9611  5     57815 404.24 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

---
template: test_complet

## Test de l'égalité des pentes 
--

`$$\begin{align} 
H_0 & =\left \lbrace \mbox{La longueur des ailes augmente de la même manière avec le poids quelque soit l'espèce }\right\rbrace\\
    & =\left \lbrace  \mbox{pour tout }i, \gamma_i = 0   \right\rbrace\\
    & =\left \lbrace  M_{comp} \mbox{ est équivalent à } M_{12} \right\rbrace.
\end{align}$$`

`$$M_{12} : \class{alea}{Y_{ik}} = \class{rouge}{\mu} + \class{rouge}{\alpha_i} + \class{rouge}{\beta}x_{ik} + \class{alea}{E_{ik}},\quad \class{alea}{E_{ik}}\overset{ind}{\sim}\mathcal{N}(0, \class{rouge}{\sigma^2})$$`
--

`$$\begin{align} 
H_1 & =\left \lbrace \mbox{L'augmentation de longueur des ailes avec le poids n'est pas la même pour toutes les espèces}\right\rbrace\\
    & =\left \lbrace  \mbox{Il existe un }i,\gamma_i \ne 0 \right\rbrace\\
    & =\left \lbrace  M_{comp} \mbox{ est préférable à } M_{12} \right\rbrace.
\end{align}$$`

---
template: test_complet

## Test de l'égalité des pentes

### Statistique de test 
--

`$$F = \frac{\frac{RSS_{12}-RSS}{I-1}}
{\frac{RSS}{n-2I}} \underset{H_0}{\sim} \mathcal{F}(I-1, n-2I)$$`

--
2 situations :
* si les pentes sont différentes, on a mis en évidence un effet de l'espèce et un effet de la masse ne serait ce qu'au travers de leur interaction.

* si les pentes sont identiques, le modèle `$M_{12}$` devient alors le modèle le plus complet considéré et on teste si la pente est différente de 0 et on teste si les ordonnées à l'origine sont identiques.

Quels modèles peut on comparer ?

---
template: test_complet

## Test de l'égalité des pentes sur l'exemple manchots

```r
M12 <- lm(flipper_length_mm ~ species + body_mass_g, data =penguins)
anova(M12, Mcomp)
```

```
## Analysis of Variance Table
## 
## Model 1: flipper_length_mm ~ species + body_mass_g
## Model 2: flipper_length_mm ~ species + body_mass_g + species:body_mass_g
##   Res.Df    RSS Df Sum of Sq      F Pr(>F)  
## 1    338 9839.1                             
## 2    336 9611.2  2    227.91 3.9837 0.0195 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

---
template: test_complet

Que teste-t-on avec cette commande ?

```r
library(car)
```

```
## Warning: package 'car' was built under R version 4.0.5
```

```
## Loading required package: carData
```

```
## 
## Attaching package: 'car'
```

```
## The following object is masked from 'package:dplyr':
## 
##     recode
```

```
## The following object is masked from 'package:purrr':
## 
##     some
```

```r
Anova(Mcomp)
```

```
## Anova Table (Type II tests)
## 
## Response: flipper_length_mm
##                     Sum Sq  Df  F value Pr(>F)    
## species             6411.2   2 112.0661 <2e-16 ***
## body_mass_g         5114.2   1 178.7885 <2e-16 ***
## species:body_mass_g  227.9   2   3.9837 0.0195 *  
## Residuals           9611.2 336                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

---
name: ajuste

# Comparer les espèces à poids équivalents

La répondre à la question "Les longueurs des ailes des manchots des différentes espèces sont-elles comparables"

Pour rendre la comparaison juste, il faut choisir un poids de référence.

Moyenne ajustée

`$$\hat{\mu}_i = \mu + \alpha_i + (\beta+\gamma_i) \bar{x}$$`

```r
library(emmeans)
```

```
## Warning: package 'emmeans' was built under R version 4.0.5
```

```
## 
## Attaching package: 'emmeans'
```

```
## The following object is masked from 'package:devtools':
## 
##     test
```

```r
mean_length <- emmeans(object = Mcomp, specs = ~ species)
```

```
## NOTE: Results may be misleading due to involvement in interactions
```

```r
pairs(mean_length, adjust = "bonf")
```

```
##  contrast           estimate   SE  df t.ratio p.value
##  Adelie - Chinstrap    -8.10 1.21 336  -6.678  <.0001
##  Adelie - Gentoo      -15.99 1.16 336 -13.733  <.0001
##  Chinstrap - Gentoo    -7.88 1.41 336  -5.582  <.0001
## 
## P value adjustment: bonferroni method for 3 tests
```

```r
plot(mean_length)
```

![](ancova_files/figure-html/ajuste-1.png)