# A tibble: 30 × 11
das alt pen deb pH dur pho nit amm oxy dbo
<dbl> <int> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.3 934 48 0.84 7.9 45 0.01 0.2 0 12.2 2.7
2 2.2 932 3 1 8 40 0.02 0.2 0.1 10.3 1.9
3 10.2 914 3.7 1.8 8.3 52 0.05 0.22 0.05 10.5 3.5
4 18.5 854 3.2 2.53 8 72 0.1 0.21 0 11 1.3
# ℹ 26 more rowsPrincipal Component Analysis
https://marieetienne.github.io/TopicsInStatistics/
2025-09-25
\[ \newcommand\R{{\mathbb{R}}} \newcommand\norm[1]{\lVert#1\rVert} \]
Introduction
The Example of Doubs River Characteristics
We measured the physico-chemical characteristics at 30 different sites along the Doubs River .
The first 4 rows (out of 30) of the doubs.env dataset
How can we best visualize these data to reveal the relationships between variables and identify similarities between sites?
- das: distance to the source (\(km\)),
- alt: altitude (\(m\)),
- pen: slope (elevation change per 1000m),
- deb: flow rate (\(m^3.s^{-1}\)),
- pH: water pH,
- dur: calcium concentration (\(mg.L^{-1}\)),
- pho: phosphate concentration (\(mg.L^{-1}\)),
- nit: nitrate concentration (\(mg.L^{-1}\)),
- amn: ammonium concentration (\(mg.L^{-1}\)),
- oxy: dissolved oxygen concentration (\(mg.L^{-1}\)),
- dbo: Biological Oxygen Demand (\(mg.L^{-1}\)).
The Example of Penguin Morphology
We measured the morphological characteristics of various penguins:
The first 6 rows (out of 333) of the penguins dataset
# A tibble: 333 × 4
bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
<dbl> <dbl> <int> <int>
1 39.1 18.7 181 3750
2 39.5 17.4 186 3800
3 40.3 18 195 3250
4 36.7 19.3 193 3450
5 39.3 20.6 190 3650
6 38.9 17.8 181 3625
# ℹ 327 more rowsHow can we best visualize these data to reveal the relationships between variables and identify similarities between individuals?
- bill_length_mm: bill length,
- bill_depth_mm: bill depth,
- flipper_length_mm: flipper length,
- body_mass_g: body mass.
Introduction
Formalization
- For each individual \(i\), we measured \(p\) different variables.
- For each variable \(k\), we measured \(n\) individuals.
The data are arranged in a table with \(n\) rows and \(p\) columns.

We denote \(x_{ik}\) as the value measured for variable \(k\) on individual \(i\),
and
- \(x_{\bullet k} = \frac{1}{n} \sum_{i=1}^n x_{ik}\) as the mean value of variable \(k\),
- \(s_k = \sqrt{\frac{1}{n} \sum_{i=1}^n (x_{ik}-x_{\bullet k})^2}\) as the standard deviation of variable \(k\).
The Same Question in Various Fields
- Sensory analysis: score of descriptor \(k\) for product \(i\)
- Economics: value of indicator \(k\) for year \(i\)
- Genomics: gene expression \(k\) for patient/sample \(i\)
- Marketing: satisfaction index \(k\) for brand \(i\)
etc…
We have \(p\) variables measured on \(n\) individuals, and we want to visualize these data to understand the relationships between variables and the proximity between individuals.
Seeing is Understanding: How to Represent the Information Contained in This Table?
Idea 1: Represent the relationships between variables 2 by 2
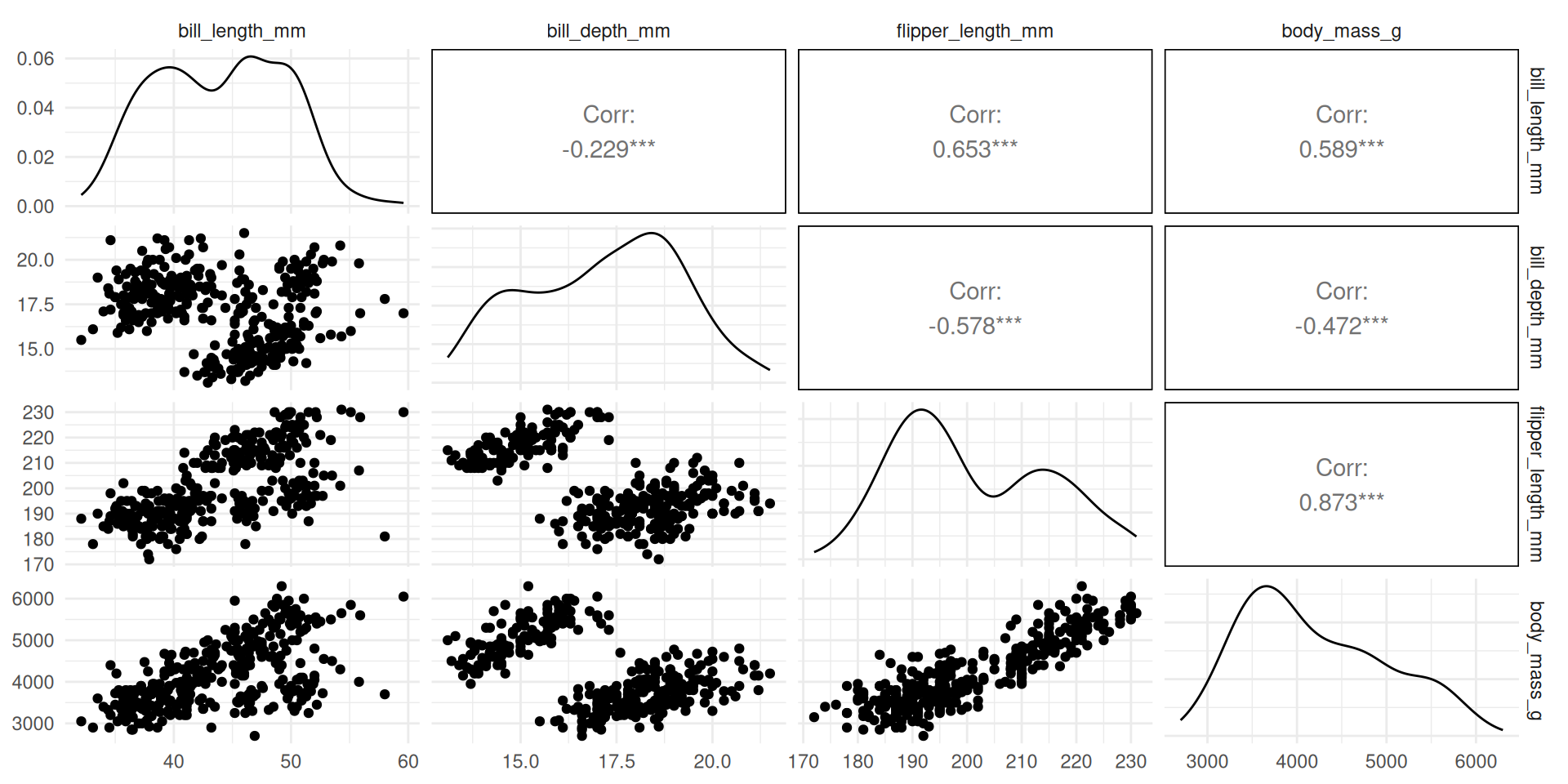
Seeing is Understanding: How to Represent the Information Contained in This Table?
Idea 1: Represent the relationships between variables 2 by 2
We lose information on the other axes.
Seeing is Understanding: How to Represent the Information Contained in This Table?
Idea 1: Represent the relationships between variables 2 by 2
Seeing is Understanding: How to Represent the Information Contained in This Table?
Objective:
- Represent without losing too much information
- Ideally, individuals far apart in the initial cloud remain far apart in the representation.
What We Need:
- Quantify the information loss in the representation
- Build the representation that loses the least amount of information
Precautions:
- Potentially, Make variables expressed in different units comparable
Distance and Inertia
Distance between individuals
Let \(X_{i,.}^\intercal \in \R^d\) be the descriptions of individual \(i\). To quantify the distance between indivuals we might used the Euclidian distance in \(\R^d,\)
\[d(i, j)^2 = \sum_{k=1}^d (x_{ik} - x_{jk})^2 = \norm{X_{i,.}^\intercal - X_{i,.}^\intercal}^2 = \left({X_{i,.}^\intercal - X_{i,.}^\intercal}\right)^\intercal \left({X_{i,.}^\intercal - X_{i,.}^\intercal}\right). \]
This could be misleading when dealing with different variables with different scale.
Example in the penguins dataset
Body mass varies form 2700 to 6300, while flipper length varies from 172 to 231.
Variable Body mass will contribute more to the distance between individuals.
Specify a different metric
Definition
A metric in \(\R^d\), \(M\) is a definite positive symmetric \(\R^{d\times d}\) matrix which can be used to define distance between individuals
\[d_M(i, j)^2 = \norm{X_{i,.}^\intercal - X_{i,.}^\intercal}^2_M = \left({X_{i,.}^\intercal - X_{i,.}^\intercal}\right)^\intercal M \left({X_{i,.}^\intercal - X_{i,.}^\intercal}\right).\]
- If \(M=I_d\),
\(d_M\) is the classical Euclidian distance
- Get rid of the units used for the variables and attribute the same weight to all variables by choosing
\(M = \begin{pmatrix} \frac{1}{s_1^2} & &0 & \cr & \frac{1}{s_2^2} & & \cr &0 & \ddots & \cr &&& \frac{1}{s_d^2} \cr \end{pmatrix} = D_{1/s^2}\)
with \(s_k^2=\sum_{i=1}^n (x_{ik} - x_{.k})^2,\) \(x_{.k} =\frac{1}{n}\sum_{i=1}^n x_{ik}\)
Remarks
The distance defined with \(D_{1/s^2}\) is the same than the distance defined on centred and scaled variables with the identity matrix.
In the following, we will assume that \(X\) is the matrix of centred and scaled variables.
Dispersion measure: Inertia with respect to a point
Definition
Inertia (denomination derived from moments of inertia in Physics) with respect to a point \(a \in R^{d},\) according to metric \(M\): \[I_a = \frac{1}{n}\sum_{i=1}^n \norm{X_{i,.}^\intercal - a}_M^2\]
- Inertia around the centroïd \(G\) (center of gravity of the cloud) plays a central role in Principal Component Analysis:
\(G = (x_{.,1}, \cdots, x_{.,d})^\intercal\) and \(I_G = min_{a\in \R^d} I_a\)
Remarks
Assume, we deal with centred scaled variables:
\(I_G = \frac{1}{n} \sum_{i=1}^n \norm{X_{i,.}^\intercal - G}^2 = \frac{1}{n}\sum_{i=1}^n \class{rouge}{\sum_{k=1}^d} (x_{ik} - x_{.,k})^2 = \class{rouge}{\sum_{k=1}^d} \frac{1}{n} \sum_{i=1}^n (x_{ik} - x_{.,k})^2.\)
As the variables are scaled, $ {i=1}^n (x{ik} - x_{.,k})^2 = s^2_k = 1.$ and \(I_G=d.\)
Total inertia with scaled centred variables is \(d\)
Dispersion measure: Inertia with respect to a affine subspace
Definition
Inertia with respect to an affine subspace \(S\) according to metric \(M\): \(I_S = \sum_{i=1}^n d_M(X_{i,.}, S)^2\)
Huygens theorem states that if \(S^G\) stands for the affine subspace containing \(G\) and parallel to \(S\) then \[I_S = I_{S^G} + d_M^2(a, G),\] where \(a\) is the orthogonal projection of \(G\) on \(S\).
The affine subspace \(S\) which minimizes inertia is \(S^G\).
Inertia Decomposition
Since, variables are centred \(G=\mathbb{0}\), \(I= \frac{1}{n} \sum_{i=1}^n d(X_{i,.},0)^2.\)
Let \(S\) be an affine subspace and \(U=S^\intercal,\) \(X^S_{i,.}\) (recip. \(X^S_{i,.})\)) the orthogonal projection on \(S\) (recip. on \(U\)).
As \(d(X_{i,.},0)^2 = d(X^S_{i,.},0)^2 + d(X^U_{i,.},0)^2\), \(I=I_S + I_{S^\intercal}\)
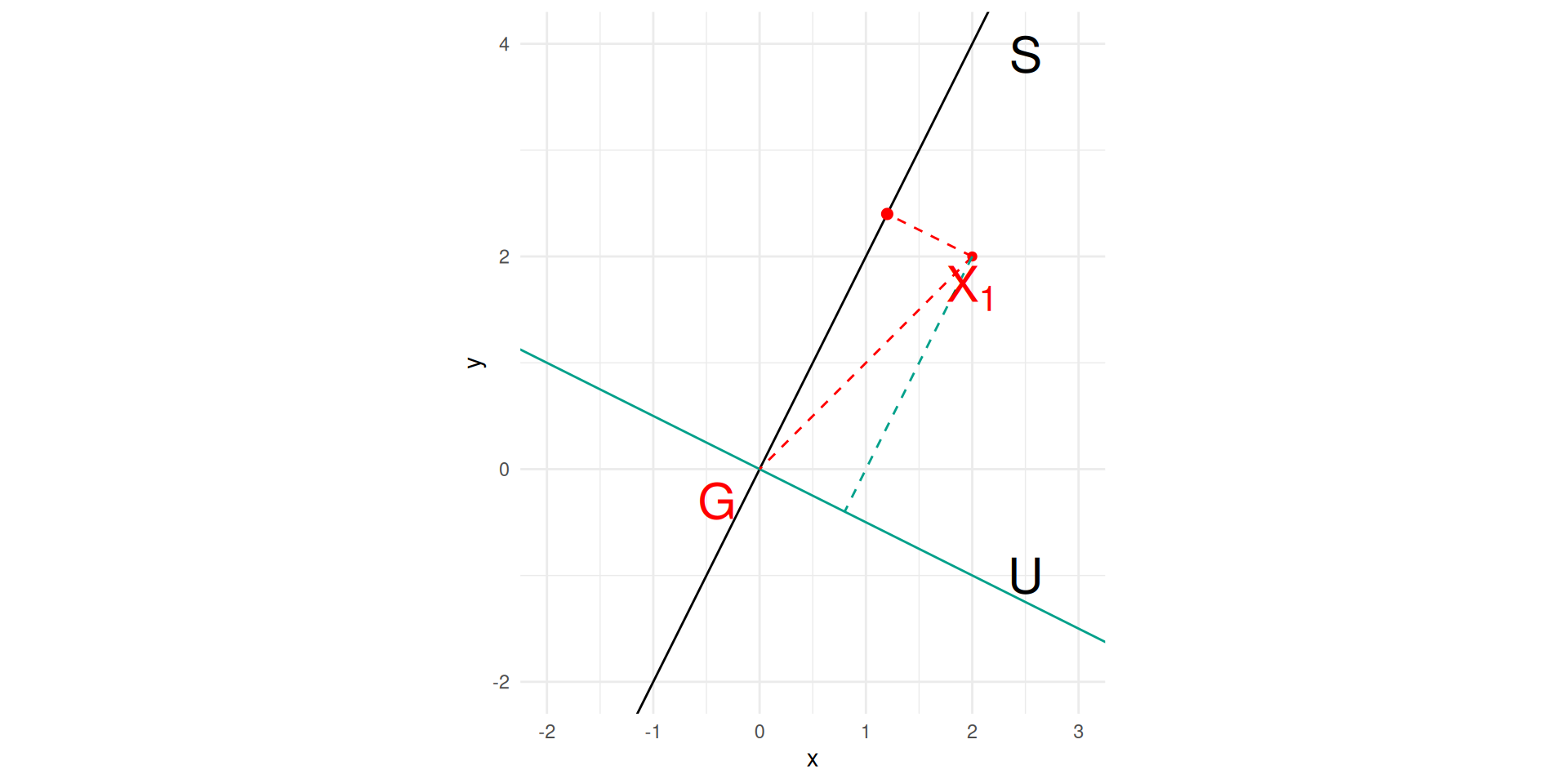
Interpretation
\(I_S\) is the dispersion of the dataset lost by projection on \(S\),
while \(I_{S^\intercal}\) is the dispersion of the dataset projected on \(S\).
PCA
Identifying \((U_1, U_d)\) a sequence of orthogonal unitary vectors such that \(I_{U_1}\leq I_{U_2}\leq \cdots \leq I_{U_d}\).
The projection on \(U_1\) is the best projection of the dataset in one dimension, \(U_1\) define the first Principal Component.
Inertia: useful representation
Let \(x_i= X_{i,.}^\intercal\), (recall that \(X_{i,}\) is a row vector and \(x_i\) is the corresponding column vector).
\[\begin{align} I & = \frac{1}{n} \sum_{i}^n d^2(X_{i,.}, 0) = \frac{1}{n} \sum_{i}^n \norm{X_{i,.}}\\ & = \frac{1}{n} \sum_{i}^n x_i^\intercal x_i \cr & = tr( \frac{1}{n} \sum_{i}^n x_i^\intercal x_i) \cr & = tr( \frac{1}{n} \sum_{i}^n x_i x_i^\intercal ) \cr & = tr( \frac{1}{n} X^\intercal X) \cr \end{align}\]
Remarks
\(\frac{1}{n} X^\intercal X\) is the covariance matrix of the \(d\) variables,
\(\frac{1}{n} X^\intercal X\) is a symmetric \(\R^{d\times d}\) matrix, and the corresponding SVD, might be derived from the SVD of \(\frac{1}{\sqrt{n}}X\):
\[ \frac{1}{\sqrt{n}}X = P D Q^\intercal\]
\[\frac{1}{n} X^\intercal X = \left ( P D Q^\intercal \right )^\intercal \left ( P D Q^\intercal \right ) = Q D P^\intercal P D Q^\intercal = Q D^2 Q^\intercal.\]
\(I= tr( \frac{1}{n} X^\intercal X) = tr(Q D^2 Q^\intercal) = tr(Q^\intercal Q D ) = tr( D ) = \sum_{k=1}^d \sigma^2_k,\)
where \(\sigma^2_k\) stands for the k\(^{th}\) eigen value.
Principal Components Construction
Current Objective
We seek \(\boldsymbol{u_1}\) such that \(I_{u_1}\) is minimal but \(I_{u_1} + I_{u_1^\perp}=I\). Minimizing \(I_{u_1}\) is equivalent to maximizing \(I_{u_1^\perp}\), i.e. the inertia of the projected cloud.
- The first individual is projected as \(\class{alea}{x_{1}}^\top \boldsymbol{u_1}\) onto \(\boldsymbol{u_1}\)
- The second individual is projected as \(\class{alea}{x_{2}}^\top \boldsymbol{u_1}\) onto \(\boldsymbol{u_1}\)
- …
Recall that \[{\boldsymbol{X}}= \begin{pmatrix} \class{alea}{x_{1}}^\top \\ \vdots \\ \class{alea}{x_{n}}^\top \end{pmatrix}.\] The projection of individual \(i\) is obtained by multiplying the row vector \(\class{alea}{x_{i}}^\top\) by \(\boldsymbol{u_1}\). The vector of coordinates on \(\boldsymbol{u_1}\) for each individual is
\[\begin{pmatrix} \class{alea}{x_{1}}^\top \boldsymbol{u_1} \\ \vdots \\ \class{alea}{x_{n}}^\top \boldsymbol{u_1} \end{pmatrix} = X \boldsymbol{u_1}.\]
Maximize \(I_{u_1^\perp}\)
under the constraint \(\lVert\boldsymbol{u_1}\rVert\) \[\begin{align} I_{u_1^\perp} & = \frac{1}{n}\lVert X \boldsymbol{u_1}\rVert^2 \\ & = \frac{1}{n} (X \boldsymbol{u_1})^\top (X \boldsymbol{u_1})\\ & = \boldsymbol{u_1}^\top \left (\frac{1}{n} X^\top X \right) \boldsymbol{u_1} \end{align}\]
Formally
\(\frac{1}{n} X^\top X\) is the covariance matrix, often written as \(X^\top W X\) (\(W\) is a diagonal matrix, with each diagonal entry equal to \(1/n\), \(W_{ii}\) is the weight assigned to observation \(i\)).
Considering the SVD of \(X\), we have \(X= P^\intercal D Q\) and so \[\frac{1}{n} X^\top X = X^\top W X = Q^\intercal D^2 Q.\]
The diagonal entries of \(D\) are the eigenvalues, all positive, of \(X^\top W X\), arranged in decreasing order, \(\lambda_1 > \lambda_2 \ldots >\lambda_p\), and \(U\) is the matrix of the associated eigenvectors.
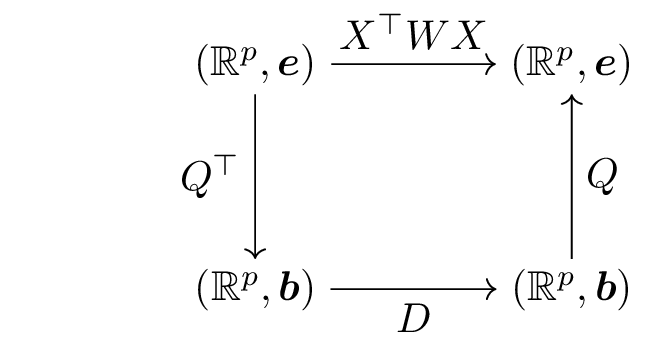
\(\boldsymbol{b}\) is an orthonormal basis, the basis formed by the eigenvectors of \(X^\top W X\).
Identify \(\boldsymbol{u_1}\) - Formalization
SVD of \(X^\intercal X\) instead of \(X\)
As we are mainly interesting in \(Q\), \(d\times d\) matrix (not \(P\) the \(n\times n\) matrix) and the square of the eigen values, it is more efficient to consider the SVD of \(\Sigma\) directly.
Geometrically
The matrix \(Q^\intercal\) transform the original canonical basis \((e_1, \cdots, e_d)\) of \(\R^d\) in the new ACP basis \((v_1, \cdots, v_d)\); .
In the new basis variable \(k\),
\[ \sum_{j=1}^d \sqrt{\sigma_j^2} q_{kj} v_j = \begin{pmatrix} \sigma_1 q_{1j}, \cdots, \sigma_d q_{dj} \end{pmatrix}^\intercal\]
Palmer Penguins example
## the core scale function normalizes by n-1 instead of n
scale2 <- function(x, na.rm = FALSE) (x - mean(x, na.rm = na.rm)) / ( sqrt((length(x)-1) / length(x)) *sd(x, na.rm) )
X <- penguins |>
mutate(year = as.factor(year))|> ## year will not be considered as numerical variable
select(where(is.numeric)) |> ## select all numeric columns
mutate_all(list(scale2)) ## and scale them
n <- nrow(X) # number of individuals
d <- ncol(X)
X_mat <- X |> as.matrix() ## the data point matrix
X_norm_mat <- 1/sqrt(n) * X_mat ## the version considered to get rid of the number of individuals
X_norm_mat_trace <- sum( diag( t( X_norm_mat)%*% X_norm_mat ) ) # the trace of the covariance matrix
penguins_norm_svd <- svd( t(X_norm_mat)%*% X_norm_mat )
## eigenvalues
penguins_norm_eigenvalue <- penguins_norm_svd$d
sum(penguins_norm_eigenvalue)[1] 4Palmer Penguins example
penguins_norm_Q <- penguins_norm_svd$u
## From orginal variable to new basis
## t(Q) %*% t(X[1,]) for 1st individual
## t(Q) %*% t(X) for all individuals, or in order to keep individual in lines
## X %*% Q
coord_newbasis <- X_mat %*% (penguins_norm_Q)
coord_newbasis <- coord_newbasis |>
as_tibble() |>
rename(Dim1 = V1, Dim2 = V2, Dim3 = V3, Dim4 = V4)
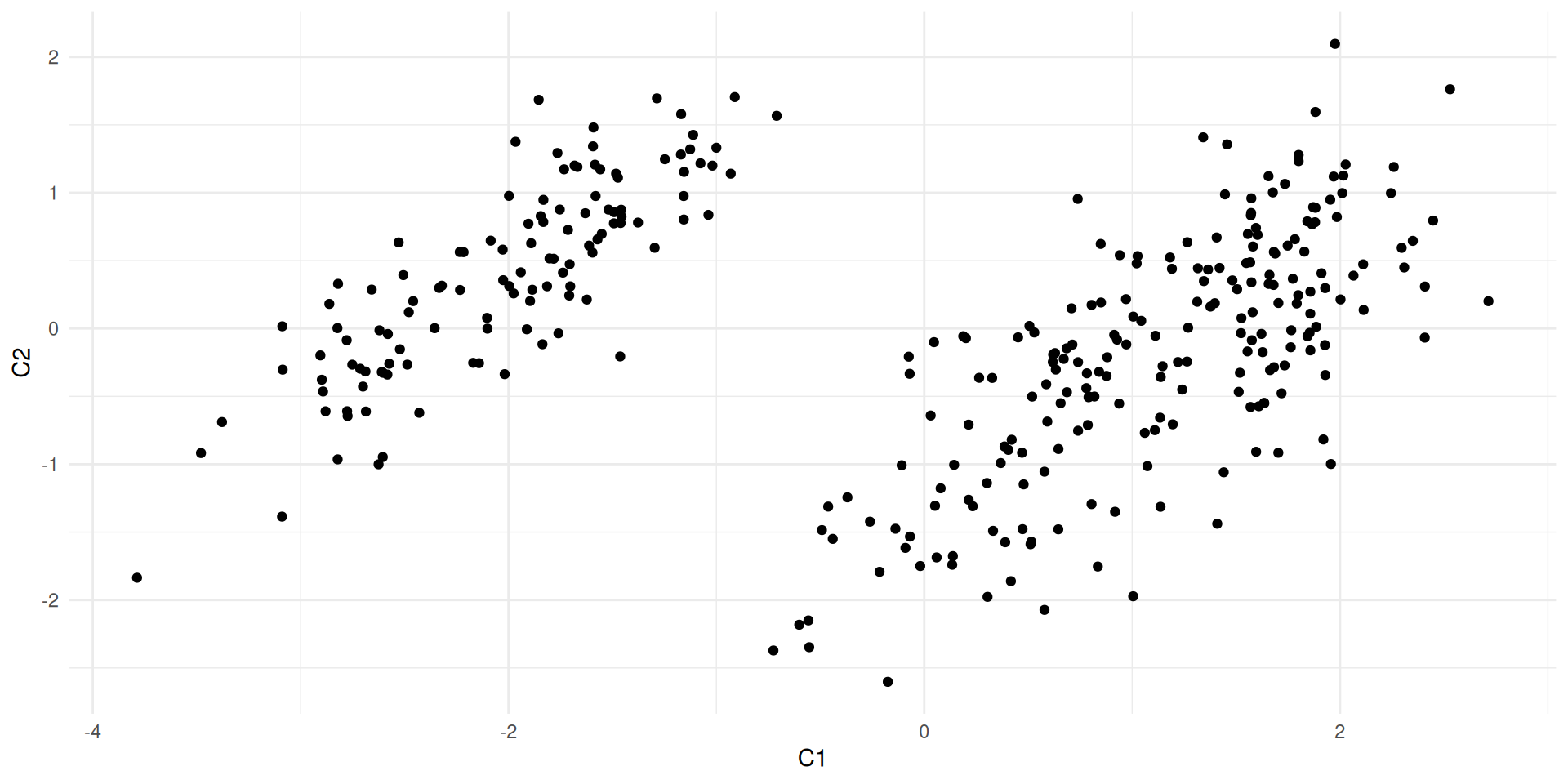
ggplot(coord_newbasis) + aes(x= Dim1, y = Dim2) + geom_point()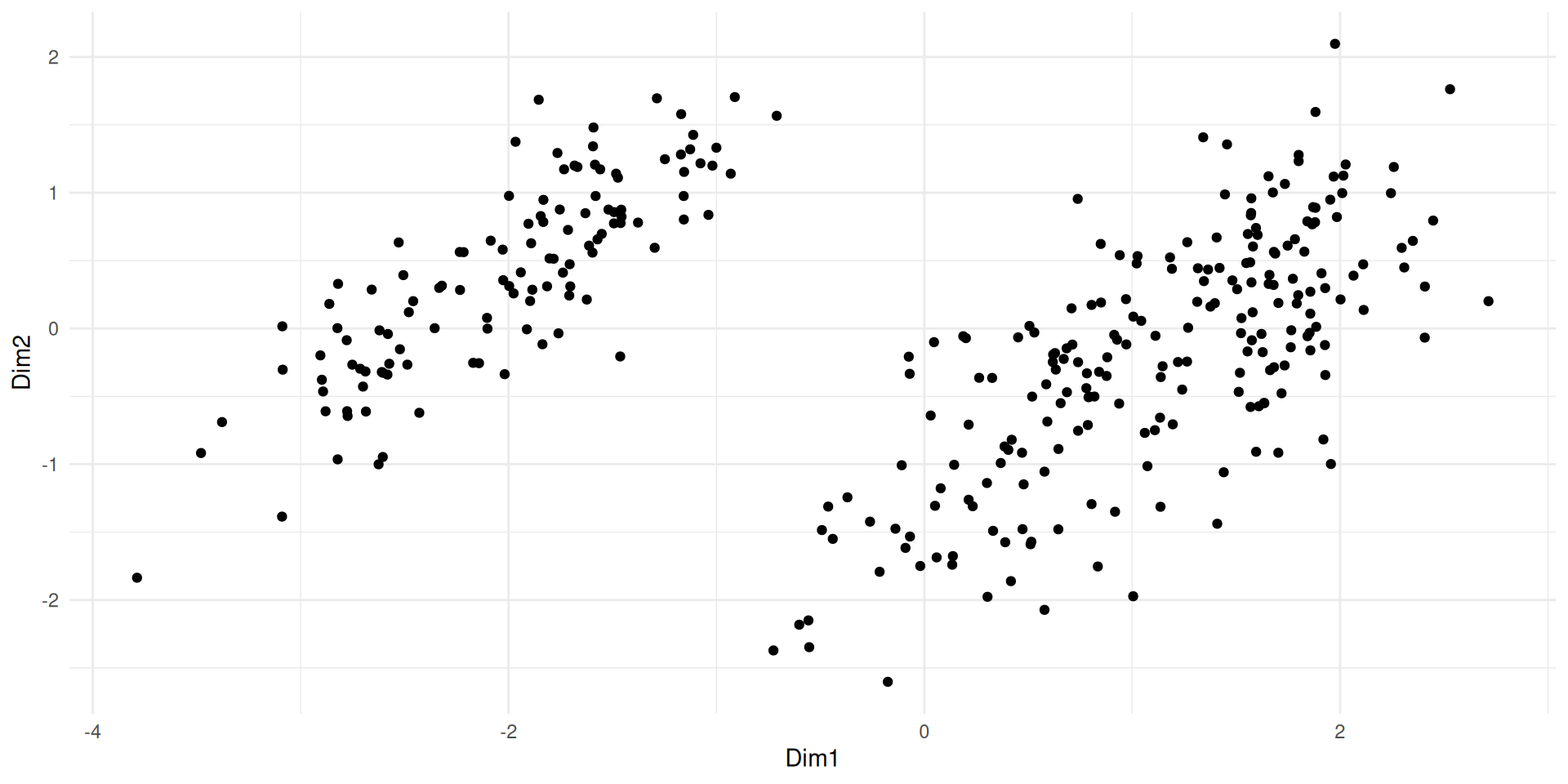
#ggplot(coord_newbasis) + aes(x= Dim1, y = Dim2) + geom_point()
dist(X[1:5,])
dist(coord_newbasis[1:5,])
dist(coord_newbasis[1:5,])
dist(coord_newbasis[1:5,1:2])
#dist(coord_norm_newbasis[1:5,]) * sqrt(n)
X_C <- as.matrix(coord_newbasis) 1 2 3 4
2 0.7576266
3 1.2500130 0.9980553
4 1.0773914 1.2792018 0.9767689
5 1.1679522 1.6632525 1.4687302 0.8784467
1 2 3 4
2 0.7576266
3 1.2500130 0.9980553
4 1.0773914 1.2792018 0.9767689
5 1.1679522 1.6632525 1.4687302 0.8784467
1 2 3 4
2 0.7576266
3 1.2500130 0.9980553
4 1.0773914 1.2792018 0.9767689
5 1.1679522 1.6632525 1.4687302 0.8784467
1 2 3 4
2 0.7175826
3 0.5146672 0.2886753
4 0.0545691 0.7139414 0.5300224
5 0.7883291 1.3981852 1.1195367 0.8306741Global quality of the representation
Let \(C_{12}\) designs the plan defined by \(C_1\) and \(C_2\) and let \(X^{C}\) be the coordinates of the individuals in the new basis.
The information preserved by projection is \[\begin{align} I_{C_{12}^\perp} & = \sum_{i=1}^n \left ( \left(x^{C}_{i1)}\right)^2 + \left(x^{C}_{i2}\right)^2 \right) \cr & = tr\left( \left(X^{C}_{,1:2}\right)^\intercal X^{C}_{,1:2}\right)\cr & = \lambda_1^2 + \lambda^2_2\cr & = n (\sigma_1^2 + \sigma^2_2)\cr \end{align}\]
cat("Working with the correlation matrix (/n), sum of eigenvalues is ", sum(penguins_norm_eigenvalue[1:2]), ". \n This has to be multiply by the size of the dataset to get inertia:", sum(penguins_norm_eigenvalue[1:2]) * n, "\n")
cat("This is easier to appreciate when expressed as a propotion of total inertia:", round(sum(penguins_norm_eigenvalue[1:2])/sum(penguins_norm_eigenvalue)*100,2),"%. \n")Working with the correlation matrix (/n), sum of eigenvalues is 3.523473 .
This has to be multiply by the size of the dataset to get inertia: 1173.316
This is easier to appreciate when expressed as a propotion of total inertia: 88.09 %. Representing jointly initial variables and principal components
To understand the links between original and new variables, or between original variables themselve.
new_var_coord <- diag(sqrt(penguins_norm_eigenvalue))%*%t(penguins_norm_Q)
## for graphical purpose
new_var_coord_df <- t(new_var_coord) |> as_tibble() |> rename(C1=V1, C2= V2, C3 =V3, C4 = V4)
circle_df <- data.frame(theta = seq(0, 2*pi, length.out = 501)) |>
mutate(x = cos(theta), y = sin(theta))
ggplot(new_var_coord_df) + geom_point(aes(x=C1, y=C2)) + coord_fixed() + xlim(c(-1,1)) + ylim(c(-1,1)) +
geom_segment(aes(x=rep(0,4), y = rep(0,4), xend=C1, yend = C2), arrow = arrow(length = unit(0.5, "cm"))) +
geom_path(data = circle_df, aes(x=x, y=y)) +
annotate("text", label = colnames(X), x = new_var_coord_df$C1 + 0.05, y = new_var_coord_df$C2- 0.05)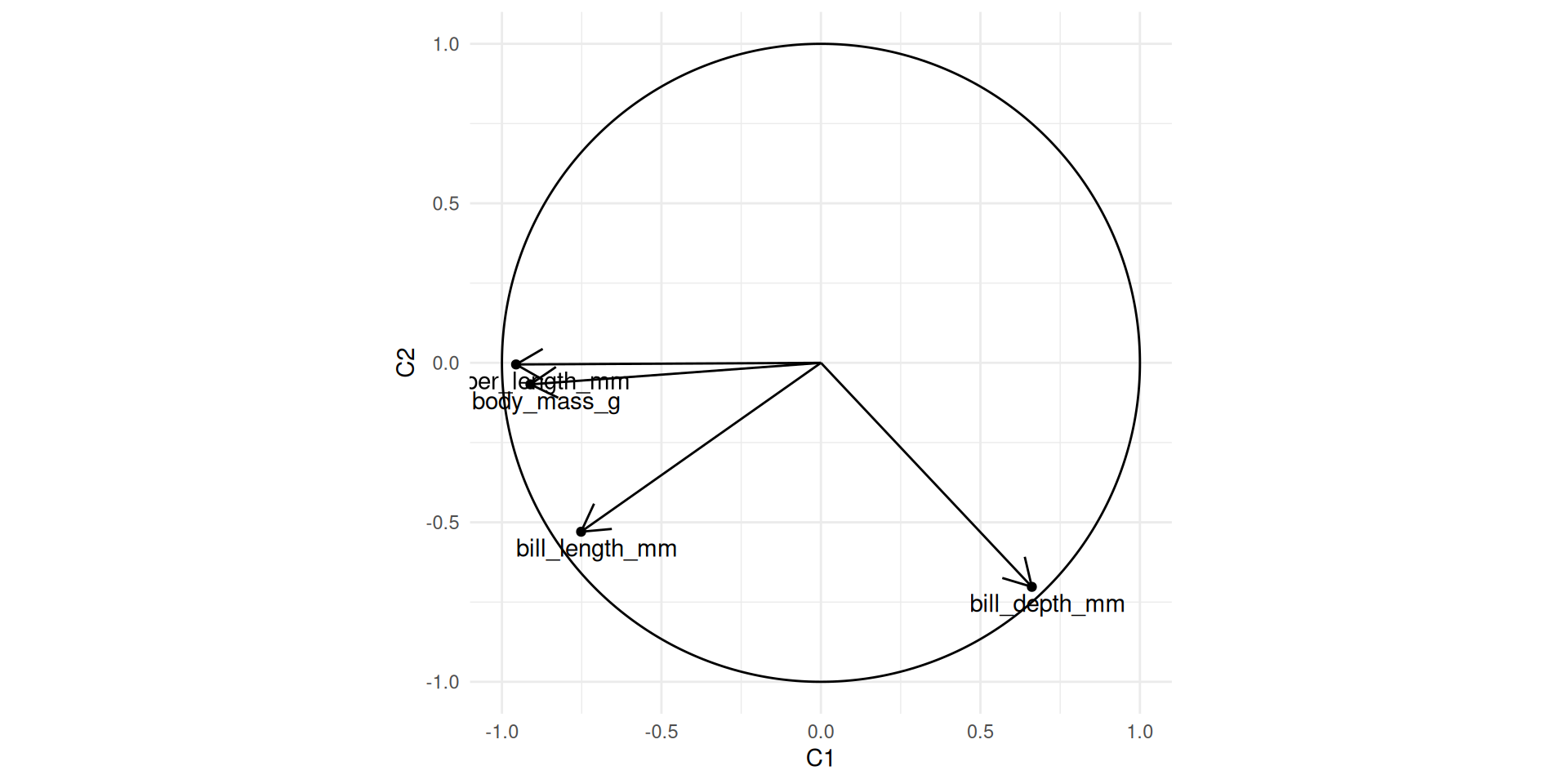
Quality fo the representation of the variables
- The quality of the projection on a component \(j\) depends on the angle \(\theta_{ij}\) between the original variable and \(C^j\).
\[cos(\theta_{ij})^2 = \frac{(C_j^T X^i)^2}{\norm{X^i}\norm{X^i}} = \sigma^2_j q_{ij}^2\]
- The quality of the projection on a the plan \((C^1C^2)\) depends on the angle \(\theta_{i,1-2}\) between the original variable and the projection plan.
\[ cos(\theta_{i,1-2})^2 = \sum_{j=1}^2 \frac{(C_j^T X^i)^2}{\norm{X^i}\norm{C^j}} = \sum_{j=1}^2 \sigma^2_j q_{ij}^2\]
Visualizing individuals
\(X\) is the matrix of individuals on the original basis, \(XQ\) is the matrix of individual in the new basis (no information lost)
To visualizing the dataset, we can project on the two first dimensions of the new basis
Interpretation
Quality of representation of individual \(i\) on the plan
- The angle between the original individual vector \(i\) and component \(j\):
\[cos(\theta_{ij})^2 = \frac{( X_i Q^j)^2}{\norm{X_i}^2} \]
Contribution to the axe \(C_i\)
The total inertia on component \(1\) is \(\sigma^2_i = \sum_{i=1}^n (XQ)_{i1}^2\).
Individual \(i\) contributes for \((XQ)_{i1}^2/\sigma^2_i\)
Practically speaking
It is way simpler !!!
You can have a look at the book Husson, Lê, and Pagès [HLP11] and visit François Husson MOOC, author of the FactoMineR package.
# install.packages('FactoMineR')
# install.packages('FactoShiny')
library(FactoMineR)
dta <- penguins |> drop_na() |> select_if(where(is.numeric)) |> select(!year)
penguins_pca <- PCA(dta, ncp = ncol(X), graph = FALSE, scale.unit = TRUE)
penguins_pca$eig
penguins_pca$var
penguins_pca$ind
plot(penguins_pca, axes = c(1,2), choix = "ind")
plot(penguins_pca, axes = c(1,2) , choix = "var")