class: center, middle, inverse, title-slide # Rappel sur quelques lois de probabilité ### Marie-Pierre Etienne, Etienne Rivot ### <a href="https://marieetienne.github.io/bayesian_and_ecology" class="uri">https://marieetienne.github.io/bayesian_and_ecology</a> ### November 2018 (updated: 2023-11-20) --- --- name: continue # Lois continues -- ## Loi exponentielle La loi exponentielle a pour support `\(\left[0,+\infty\right[\)`. `\(X\)` suit une loi exponentielle de paramètre `\(\lambda\)` si elle a pour densité `$$[X=t]=\left\lbrace \begin{array}{l} \lambda exp(-\lambda \,t) \quad t\geq 0,\cr 0 \quad sinon\cr \end{array}\right.$$` L'espérance et la variance sont données par `$$\mathbb{E}(X)=\frac{1}{\lambda} \quad \mbox{et}\quad \mathbb{V}(X)=\frac{1}{\lambda^2}.$$` --- template: continue ## Loi exponentielle 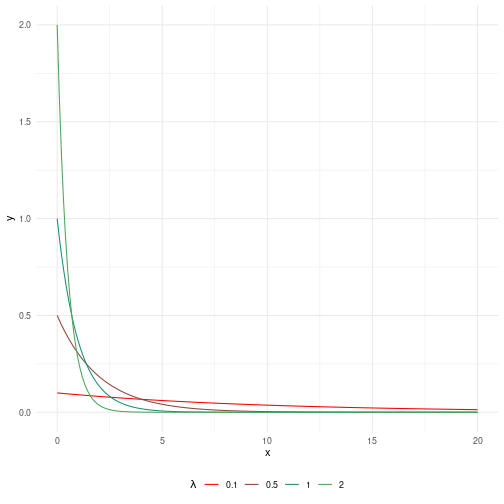<!-- --> --- template: continue ## Loi Gamma et Inverse Gamma Si `\(Y_1, \ldots, Y_n\)` sont des variables i.i.d de loi exponentielle de paramètre `\(\lambda\)` alors `\(X=\sum_{i=1}^n Y_i\)` suit une loi Gamma de paramètres de forme `\(n\)` et de paramètre d'échelle `\(\lambda\)`. On peut généraliser la définition à un `\(n\)` non entier. Le support d'une loi Gamma est `\(\left[0,+\infty\right[\)` et si `\(X\)` suit une loi `\(\Gamma(a,b)\)`, sa densité est donnée par~: `$$[X=t]=\left\lbrace \begin{array}{l} \frac{b^a t^{a-1} e^{-b\, t}}{\Gamma(a)} \quad t\geq 0,\cr 0 \quad sinon\cr \end{array}\right.$$` L'espérance et la variance sont données par `$$\mathbb{E}(X)=\frac{a}{b} \quad \mbox{et}\quad \mathbb{V}(X)=\frac{a}{b^2}.$$` --- template: continue ## Loi Gamma et Inverse Gamma Quelques exemples de lois Gamma pour différentes valeurs de `\(a\)` et `\(b\)`~: 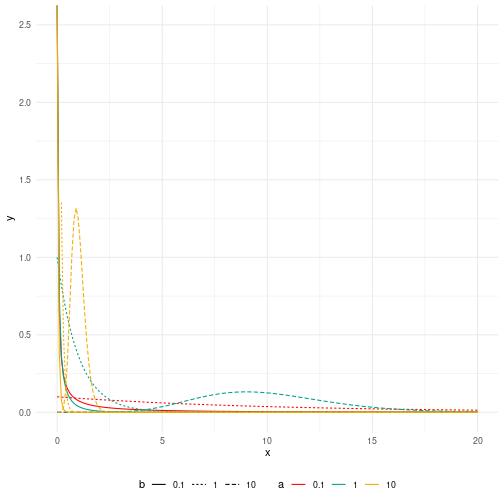<!-- --> --- template: continue ## Loi Gamma et Inverse Gamma On dit que `\(X\)` suit une loi Inverse-Gamma si `\(X^{-1}\)` suit une loi Gamma. Par ces propriétés mathématiques, la loi Inverse Gamma est naturellement candidate comme prior pour le paramètre de variance dans un modèle normal. En effet si `\(Y\sim\mathcal{N}(\mu,\sigma^2)\)` avec `\(\mu\)` connu et `\(\sigma^2 \sim \Gamma(a,b)\)`, alors `\(\sigma^2\vert Y,\mu \sim \Gamma(a',b')\)`. --- template: continue ## Loi beta La loi Beta a pour support `\(\left[0,\right]\)`. Si `\(X\)` suit une loi beta de paramètre `\((a,b)\)` alors la densité de `\(X\)` est donnée par `$$[X=t]=\left\lbrace \begin{array}{l} \frac{\Gamma(a+b) t^{a-1} (1-t)^{b-1} }{\Gamma(a)\Gamma(b)} \quad t\in [0,1] ,\cr 0 \quad sinon\cr \end{array}\right. $$ L'espérance et la variance sont données par `$$\mathbb{E}(X)=\frac{a}{a+b} \quad \mbox{et}\quad \mathbb{V}(X)=\frac{a\,b }{(a+b)^2 (a+b+1)}.$$` --- template: continue ## Loi beta 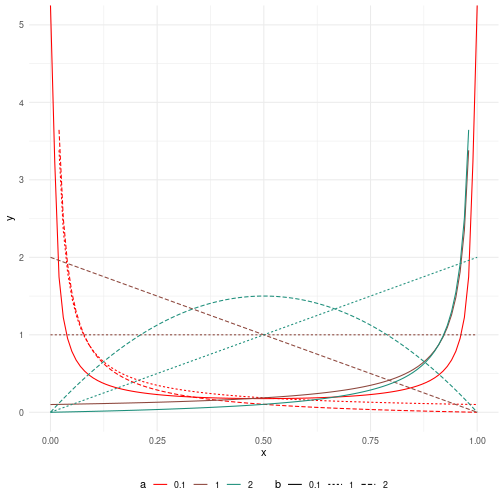<!-- --> --- name: discrete # Lois discrètes -- ## Loi binomiale .pull-left[ `\(Y\)` suit une loi de Bernoulli si le support de `\(Y\)` est `\(\left\lbrace 0,1\right\rbrace\)` et `\(\mathbb{P}(Y=1)=p\)`. Si `\(Y_1,\ldots, Y_n\)` sont des variables aléatoires indépendantes qui suivent une loi de Bernoulli de paramètre `\(p\)`, alors `\(X=\sum_{i=1}^n Y_i\)` suit une loi binomiale de paramètres `\((n,p)\)`. Le support de `\(X\)` est `\(\left\lbrace 0,1, \ldots n\right\rbrace\)` est la loi de probabilité de `\(X\)` est donnée par `$$[X=k] = {n \choose k} p^k \, (1-p)^{n-k} \qquad k \in \left\lbrace 0,1, \ldots n\right\rbrace $$ L'espérance et la variance sont données par `$$\mathbb{E}(X)=n\, p \quad \mbox{et}\quad \mathbb{V}(X)=n \, (1-p)$$` ] .pull-right[ 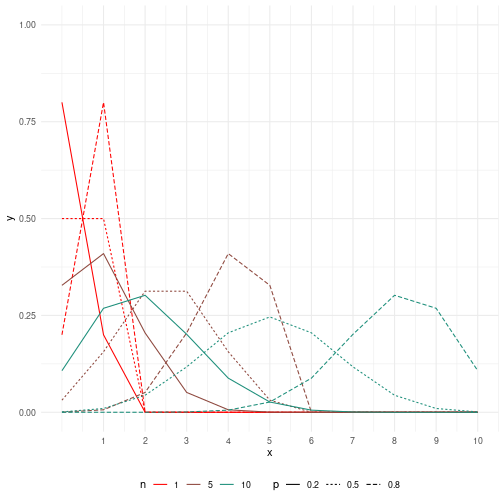<!-- --> ] --- template: discrete ## Loi de Poisson .pull-left[ Le support d'une loi de Poisson est `\(\mathbb{N}\)`. `\(X\)` suit une loi de Poisson de paramètre `\(\lambda\)` si `$$[X=k]=\frac{\lambda^k}{k!}\exp{(-\lambda\, k)}\quad k \in \mathbb{N}$$` L'espérance et la variance sont données par `$$\mathbb{E}(X)=\lambda \quad \mbox{et}\quad \mathbb{V}(X)=\lambda$$` ] .pull-right[ 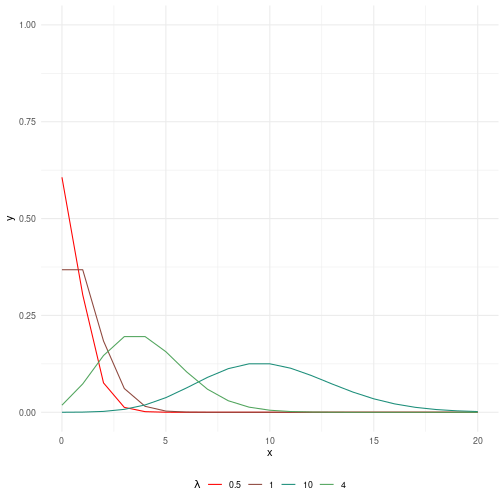<!-- --> ]