TD5 : Comparer plusieurs populations
UP Mathématique appliquée
Objectifs de la séance
- Manipulation de données
- Grouper les données par niveau d’un facteur
- Effectuer des calculs par niveau du facteur
- Visualisation de données
- Boîte à moustaches
- Analyse de données
- Démarche statistique
- Reconnaître le contexte d’une analyse de la variance
- Ecrire le modèle correspondant
- Mettre en oeuvre le test du modèle complet
Exercices
Formaliser un modèle
Pour chacune des situations ci dessous répondre aux 4 questions suivantes :
Indiquer l’individu statistique,
Indiquer la variable à expliquer et la variable explicative, en précisant leur nature.
Ecrire le modèle le plus complexe (M1).
Indiquer le modèle nul (M0) correspondant.
Situation 1
Durant 10 jours, on a noté pour 3 chaînes de production différentes les poids de volailles valorisés dans la journée. On a donc 10 mesures de poids pour chaque chaîne de production. On se demande si les différentes chaînes sont toutes aussi efficaces.
Situation 2
Pour évaluer l’impact de complément alimentaire sur la production de lait dans un élevage bovin, on réalise l’expérimentation suivante. On choisit au hasard 40 vaches dans l’élevage. 10 vaches recoivent uniquement du fourrage, 10 vaches recoivent du fourrage et le complément alimentaire, 10 vaches recoivent du fourrage et du soja, et les 10 dernières vaches reçoivent fourrage, soja et complément.
La qualité du café
Le problème qui suit est inspiré d’un stage de fin d’études réalisé par une étudiante de la spécialisation Science des données du cursus d’ingénieur agro-alimentaire d’Agrocampus.
Un groupe industriel commercialisant du café souhaite comparer les cafés provenant de différents lieux de production à partir de leur profil de composition physico-chimique, dont une des composantes importantes est le taux de matière sèche (DM). Pour cela, il s’appuie sur des données contenant le lieu de production, codé par un entier allant de 1 à 7, de 240 mesures de café disponible sur l’onglet Scripts et données de la page d’accueil du module.
Description du jeu de données sur la qualité du café
Importation du jeu de données
Importer le jeu de données
cafe_DM.csvdisponible sur la page des jeux de données dans un objet nommécafeen utilisant un scriptTD5_script.Rque vous aurez créé dans votre répertoire de projet.Utiliser la commande
summarypour obtenir un descriptif des données
R traite la variable Localisation, un entier compris entre 1 et 7, comme une variable quantitative. Il faut indiquer à R que cette variable est en fait une variable qualitative, un facteur.
cafe <- cafe %>%
mutate(Localisation = as.factor(Localisation))Visualisation des données
- Construire maintenant une boîte à moustaches des taux de matière sèche selon l’origine des cafés.
Calcul de statistiques descriptives
La commande suivante permet de calculer la moyenne de matière sèche pour chaque origine de café.
cafe %>%
group_by(Localisation) %>%
summarise(DM_mean = mean(DM))## # A tibble: 7 × 2
## Localisation DM_mean
## <fct> <dbl>
## 1 1 90.4
## 2 2 90.3
## 3 3 89.7
## 4 4 91.4
## 5 5 90.1
## 6 6 90.0
## 7 7 90.5- Calculer l’écart-type et la variance pour chaque origine.
Les lignes ci-dessous calculent la moyenne, l’écart type et certains quantiles pour chaque origine de café
stat_desc <- cafe %>%
group_by(Localisation) %>%
summarise(DM_mean = mean(DM),
DM_sd = sd(DM),
q05 = quantile(DM, probs = 0.05 ),
q50 = quantile(DM, probs = 0.5 ),
q95 = quantile(DM, probs = 0.95 )
)| Localisation | DM_mean | DM_sd | q05 | q50 | q95 |
|---|---|---|---|---|---|
| 1 | 90.40 | 0.44 | 89.61 | 90.51 | 91.04 |
| 2 | 90.26 | 0.25 | 89.86 | 90.29 | 90.58 |
| 3 | 89.69 | 0.41 | 89.08 | 89.79 | 90.28 |
| 4 | 91.37 | 0.45 | 90.70 | 91.32 | 91.90 |
| 5 | 90.13 | 0.41 | 89.70 | 90.12 | 90.57 |
| 6 | 89.99 | 0.28 | 89.54 | 89.99 | 90.37 |
| 7 | 90.50 | 0.64 | 89.71 | 90.53 | 91.37 |
Modélisation statistique
Mise en place de l’analyse statistique
- Donner l’expression du modèle statistique M\(_1\) permettant de répondre à la question ’Les taux de matière sèche diffèrent-ils d’une origine à l’autre ? Quels sont les paramètres de ce modèle ?
Ajustement du modèle
La fonction lm permet d’ajuster le modèle d’analyse de la variance.
DM_lm <- lm(DM~Localisation, data = cafe)- Donner l’expresion mathématique du modèle nul.
Il peut être ajusté grâce à la commande suivante :
DM_lm0 <- lm(DM~1, data = cafe)Test de l’effet origine
- Quelles sont les hypothèses H\(_{0}\) et H\(_{1}\) du test de l’existence de différences moyennes entre les lieux de production ? Exprimer ces hypothèses à partir des paramètres du modèle de la question précédente.
On peut comparer les deux modèles grâce à la commande:
anova(DM_lm0, DM_lm)## Analysis of Variance Table
##
## Model 1: DM ~ 1
## Model 2: DM ~ Localisation
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 239 67.132
## 2 233 35.029 6 32.104 35.59 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Enfin, les paramètres estimé dans le modèle complet sont obtenus grâce à la fonction summary.
summary(DM_lm)##
## Call:
## lm(formula = DM ~ Localisation, data = cafe)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.92961 -0.23612 0.03543 0.27781 1.10409
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 90.39711 0.05483 1648.561 < 2e-16 ***
## Localisation2 -0.13620 0.09375 -1.453 0.14763
## Localisation3 -0.70775 0.09375 -7.549 9.83e-13 ***
## Localisation4 0.96924 0.12071 8.029 4.83e-14 ***
## Localisation5 -0.26318 0.09920 -2.653 0.00853 **
## Localisation6 -0.40906 0.06926 -5.906 1.23e-08 ***
## Localisation7 0.10472 0.10450 1.002 0.31731
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3877 on 233 degrees of freedom
## Multiple R-squared: 0.4782, Adjusted R-squared: 0.4648
## F-statistic: 35.59 on 6 and 233 DF, p-value: < 2.2e-16La suite de l’exercice vise à expliciter les diverses quantités qui apparaissent dans les sorties précédentes.
Les résidus quantifient pour chaque individu statistique l’écart entre la matière sèche prédite par le modèle ajusté et la matière sèche effectivement mesurée. Ils se calculent manuellement à l’aide de la suite de commande suivante :
- Expliquer l’enchainement de ces commandes
cafe_residuals <- cafe %>%
group_by(Localisation) %>%
mutate(DM_mean = mean(DM), Residuals = DM -DM_mean)La somme des carrés des écarts résiduels, notée RSS, est un indicateur de la qualité d’ajustement du modèle.
Comment calcule-t-on RSS ?
En déduire la valeur estimée de l’écart-type résiduel du modèle.
Donner l’expression du modèle nul (associé à l’absence de différences moyennes entre les lieux de production comme dans l’hypothèse \(H_{0}\) ) des taux de matière sèche. Quelle est la valeur estimée des paramètres de ce modèle ?
Que vaut la somme des carrés des écarts résiduels RSS\(_{0}\) mesurant la qualité d’ajustement du modèle nul ?
En déduire la valeur du coefficient R\(^{2}\) du modèle M\(_1\).
Test de l’effet origine sur la quantité de matière sèche
Quelle est l’expression de la statistique de test permettant de tester l’existence de différences moyennes entre les lieux de production ? Quelle est la valeur prise par cette statistique de test ?
Quelle est la distribution sous l’hypothèse H\(_{0}\), \(\mathcal{F}_{0}\), de la statistique de test \(F\) introduite à la question précédente ?
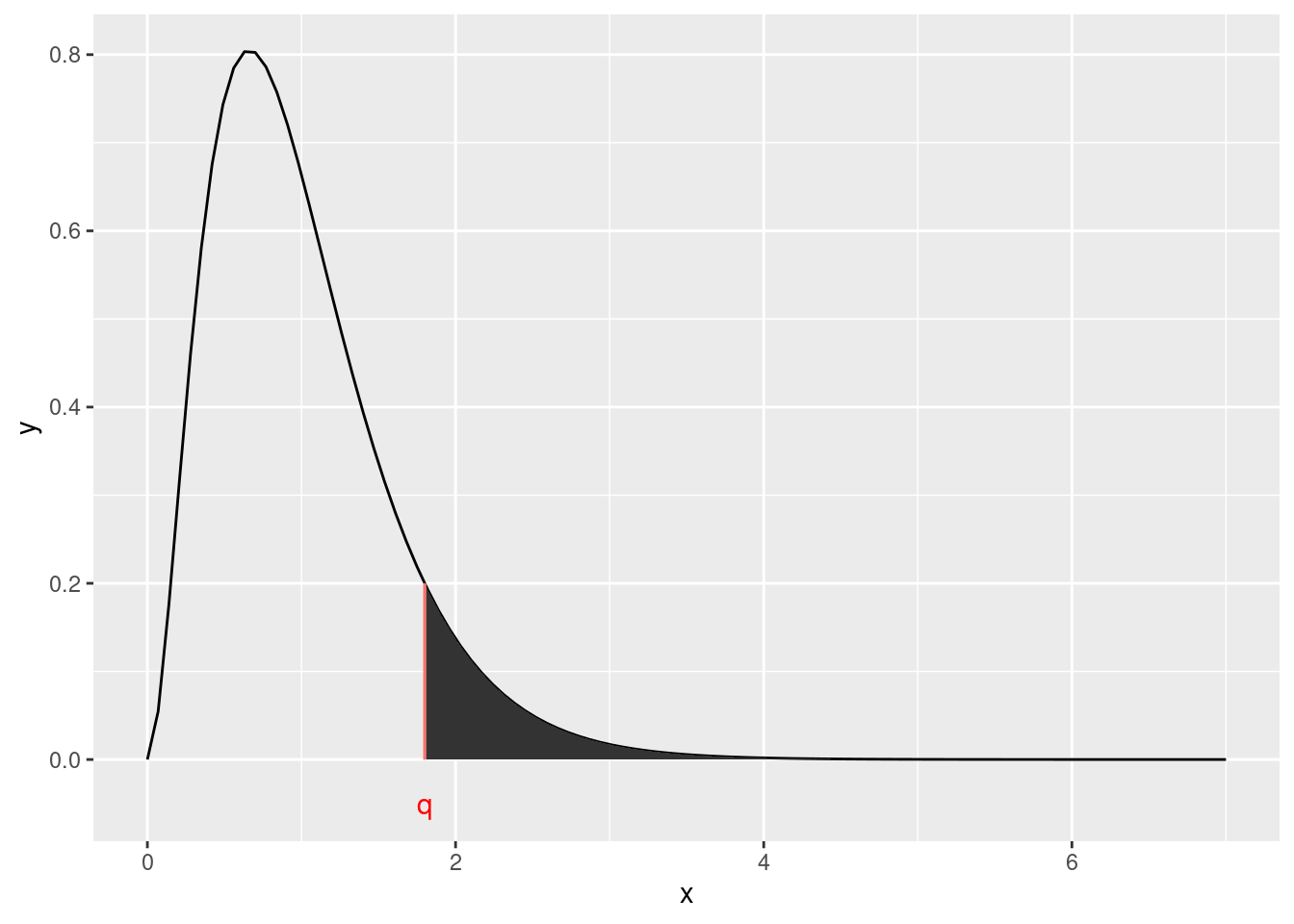
La fonction pf(q = .., df1 = .. , df2= .. , lower.tail = FALSE) donne la probabilité qu’une variable aléatoire suivant une loi de Fisher de paramètre df1, df2 dépasse la valeur q.
Conclusion de l’étude
- Donner la probabilité qu’une variable aléatoire de loi \(\mathcal{F}_{0}\) dépasse la valeur observée sur les données de café et conclure sur les différences de matière sèche en fonction de l’origine du café
Cette probabilité est la p-value.
Le vocabulaire de la séance
Commandes R
- as.factor
- group_by
- pf
- summarise
Environnement R
Statistique
- Analyse de la variance