TD8 : Comparaison de compotes
UP Mathématique appliquée
Objectifs de la séance
- Analyse de variance à 2 facteurs
- Prise en compte d’un 2ème facteur
- Puissance des tests
- Effet de la taille de l’échantillon
- Etude par simulations
Exercices
Problématique
On cherche à évaluer comment sont perçues 6 compotes de pommes au niveau de la saveur de pomme crue. Une dégustation est mise en place et 6 juges vont déguster chacune des 6 compotes. Les notes sont attribuées sur une échelle allant de 0 à 10.
La question est donc de savoir si certaines compotes sont en moyenne perçues comme ayant une plus forte saveur de pomme crue.
Analyse prenant en compte l’effet compote uniquement
Importation du premier jeu de données
- Importez le jeu de données intial
compote.csv.
Visualisation des données
- Visualiser les données pour avoir une idée des saveurs de pomme crue selon les compotes et calculez quelques statistiques descriptives par compote.
| compote | note_mean | S.pom.crue_sd | q05 | q50 | q95 |
|---|---|---|---|---|---|
| andros | 3.83 | 2.79 | 0.50 | 3.5 | 7.00 |
| carrefour | 4.33 | 2.42 | 1.50 | 4.0 | 7.00 |
| delisse | 5.83 | 2.32 | 2.75 | 6.0 | 8.50 |
| poti | 2.67 | 1.21 | 1.25 | 2.5 | 4.00 |
| scoup | 2.83 | 3.06 | 0.00 | 2.0 | 6.75 |
| st mamet | 2.83 | 2.56 | 0.25 | 2.0 | 6.00 |
Test statistique
On cherche à savoir si la saveur de pomme crue est différente selon la compote.
Test global (=Effet des facteurs)
mod1.compote <- lm(S.pom.crue ~ compote,data=dta)
mod0 <- lm(S.pom.crue~1,data=dta)
anova(mod0,mod1.compote)## Analysis of Variance Table
##
## Model 1: S.pom.crue ~ 1
## Model 2: S.pom.crue ~ compote
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 35 227.22
## 2 30 182.00 5 45.222 1.4908 0.2223Prise en compte de la variable juge
Surpris du résultat, on décide de prendre en compte la variable juge.
Visualisation
- Visualisez les notes en fonction de la compote mais en coloriant les points de couleurs différentes selon les juges.
Test statistique
- Ecrire le modèle et les hypothèses permettant de tester l’effet compote sur la saveur mais en prenant en compte l’effet du juge.
- Réaliser le test avec R.
Test global (= Effet des facteurs)
Plusieurs modèles ont été construits, et plusieurs tests sont proposés permettant de tester un modèle contre un autre.
- Dire à quelle question répond chacun des tests ci-dessous.
- Par rapport à la problématique permettant de savoir s’il y a des différences de saveur de pomme crue entre les compotes, indiquer quels tests vous allez commenter.
- Commenter et interpréter le test en lien avec votre problématique.
mod2 <- lm(S.pom.crue ~ compote + juge,data=dta)
mod1.compote <- lm(S.pom.crue ~ compote,data=dta)
mod1.juge <- lm(S.pom.crue ~ juge,data=dta)
anova(mod2,mod0)## Analysis of Variance Table
##
## Model 1: S.pom.crue ~ compote + juge
## Model 2: S.pom.crue ~ 1
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 25 69.444
## 2 35 227.222 -10 -157.78 5.68 0.0002035 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1anova(mod2,mod1.juge)## Analysis of Variance Table
##
## Model 1: S.pom.crue ~ compote + juge
## Model 2: S.pom.crue ~ juge
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 25 69.444
## 2 30 114.667 -5 -45.222 3.256 0.02121 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1anova(mod2,mod1.compote)## Analysis of Variance Table
##
## Model 1: S.pom.crue ~ compote + juge
## Model 2: S.pom.crue ~ compote
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 25 69.444
## 2 30 182.000 -5 -112.56 8.104 0.0001174 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Dans le modele mod1.compote, où se trouve la variabilité associée aux juges ? Pourquoi cela est-il gênant lorsqu’on s’intéresse à tester un effet compote ?
La fonction
Anova(avec un A majuscule) du packagecar(qu’il vous faudra sûrement installer) permet de retrouver en une seule commande les probabilités critiques de tests associés à chacun des effets. Retrouver ces probabilités critiques. Remarque : dans le cas de données déséquilibrées, les probabilités critiques obtenus avecanovaetAnovapeuvent être légèrement différentes. On préférera généralement utiliser les résultats fournis par la fonction `Anova’.
library(car)
Anova(mod2)## Anova Table (Type II tests)
##
## Response: S.pom.crue
## Sum Sq Df F value Pr(>F)
## compote 45.222 5 3.256 0.0212142 *
## juge 112.556 5 8.104 0.0001174 ***
## Residuals 69.444 25
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Test Post-Hoc (=Comparaison entre les modalités des facteurs)
library(emmeans)
comparaison_compote <- emmeans(mod2, ~ compote )
pairs(comparaison_compote)## contrast estimate SE df t.ratio p.value
## andros - carrefour -0.500 0.962 25 -0.520 0.9949
## andros - delisse -2.000 0.962 25 -2.078 0.3299
## andros - poti 1.167 0.962 25 1.212 0.8267
## andros - scoup 1.000 0.962 25 1.039 0.9000
## andros - st mamet 1.000 0.962 25 1.039 0.9000
## carrefour - delisse -1.500 0.962 25 -1.559 0.6314
## carrefour - poti 1.667 0.962 25 1.732 0.5247
## carrefour - scoup 1.500 0.962 25 1.559 0.6314
## carrefour - st mamet 1.500 0.962 25 1.559 0.6314
## delisse - poti 3.167 0.962 25 3.291 0.0314
## delisse - scoup 3.000 0.962 25 3.118 0.0462
## delisse - st mamet 3.000 0.962 25 3.118 0.0462
## poti - scoup -0.167 0.962 25 -0.173 1.0000
## poti - st mamet -0.167 0.962 25 -0.173 1.0000
## scoup - st mamet 0.000 0.962 25 0.000 1.0000
##
## Results are averaged over the levels of: juge
## P value adjustment: tukey method for comparing a family of 6 estimatesplot(comparaison_compote)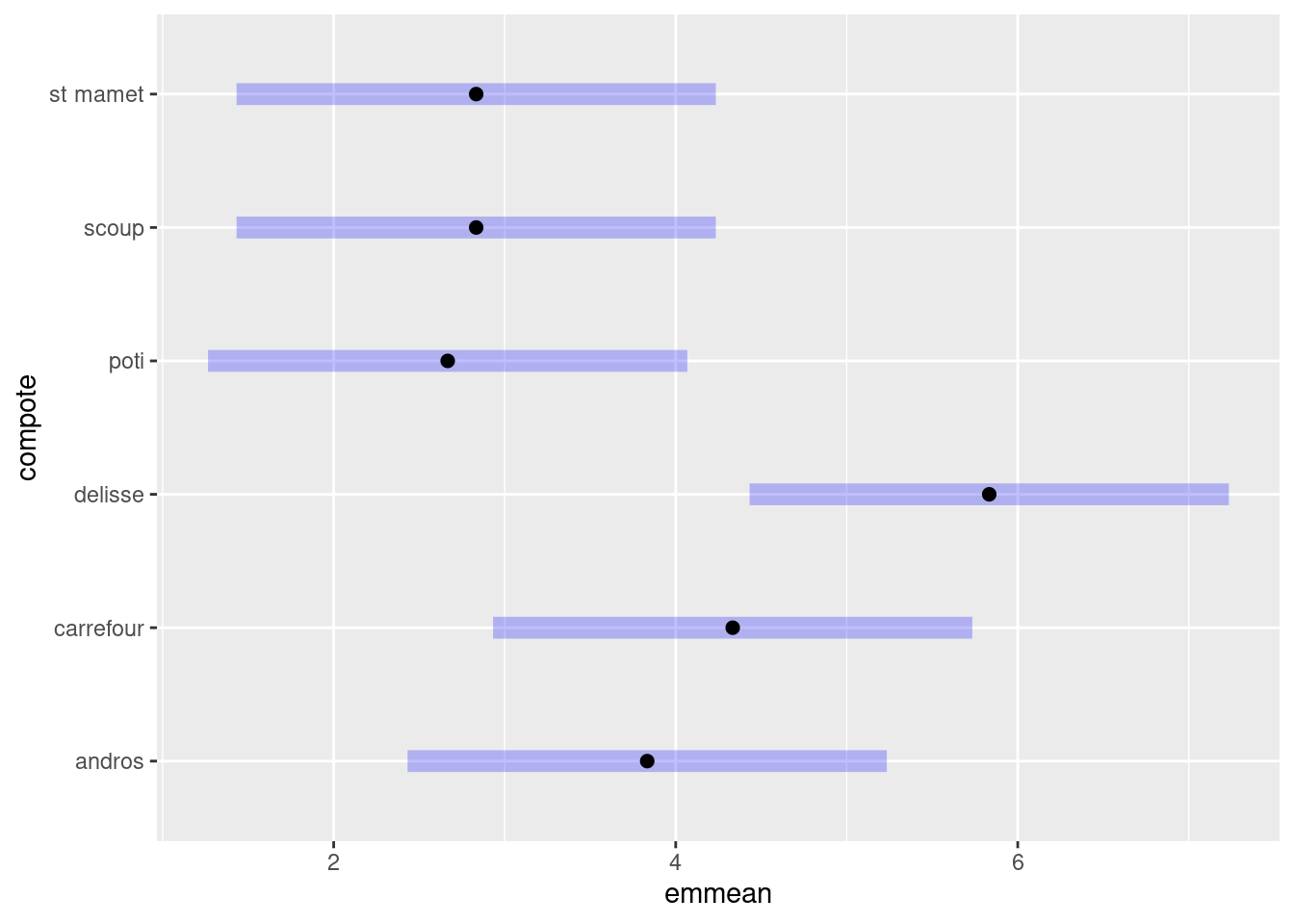
Conclusion de l’étude
Il est indispensable de lister tous les facteurs qui peuvent influer sur la variable réponse, même si ceux-ci ne sont pas intéressants à interpréter. Cela permet de réduire la variabilité résiduelle et par suite de mieux mettre en évidence l’effet potentiel qui nous intéresse.
Le vocabulaire de la séance
Commandes R
- anova et lm
- Anova (package car)
- emmeans (package emmeans)
Environnement R
Statistique
- Test d’analyse de la variance
- Test post-hoc (comparaison entre modalités d’un facteur)