Modélisation bayésienne pour l’écologie
Les slides sont disponibles
Cours Partie1 Cours Partie2
Installation logiciel
Pour les manipulations, nous aurons besoin de OpenBugs disponible ici.
Sous linux, il faut installer wine puis OpenBugs sous wine.
On va utliser également Jags disponible sous Linux et Windows et le package rjags.
Rappel sur quelques lois de probabilités utiles dans un cadre bayésien
Un petit rappel sur les lois de probabilité utiles pour la modélisation bayésienne est disponible sur la page Rappel
Application using the binomial model for capture data
While monitoring a large population of size \(n\) unknown, \(m\) individuals have been marked and released. The population might be considered as \(m\) marked individuals and \(n-m\) unmarked individuals. A recapture experiment leads to \(YM\) marked animals and \(YNM\) unmarked. What is the size of the population.
Modelling and Estimating the capture efficiency
The probability of capture might be infered from the recapture dataset and the experiment might be modelled as \[\begin{equation} YM \sim \mathcal{B}(m, p). \end{equation}\]The capture mark recapture experiment has been used for the first time on these conditions. Few is known on the probability of capture. Therefore an uniform prior is chosen to model the a priori knowledge on \(p\).
Data
m <- 53
YM <- 9Theoretical posterior distribution
Because the uniform distribution is a special case of beta distribution, the full bayesian specification for the model is a so called beta binomial model which has analytical posterior distribution.
\[\pi(p\vert YM_{obs}) \sim \mathcal{B}eta(YM + 1, m-YM +1)\]
s1 <- 1
s2 <- 1
p <- ggplot(data = data.frame(x=seq(0,1, length.out = 100)))
stat_post <- stat_function(aes(x = x, y = ..y..), fun = dbeta, colour="red", n = 100,
args = list(shape1 = YM+s1, shape2 = m-YM+s2))
stat_prior <- stat_function(aes(x = x, y = ..y..), fun = dbeta, colour="green", n = 100,
args = list(shape1 = s1, shape2 = s2))
p + stat_prior +stat_post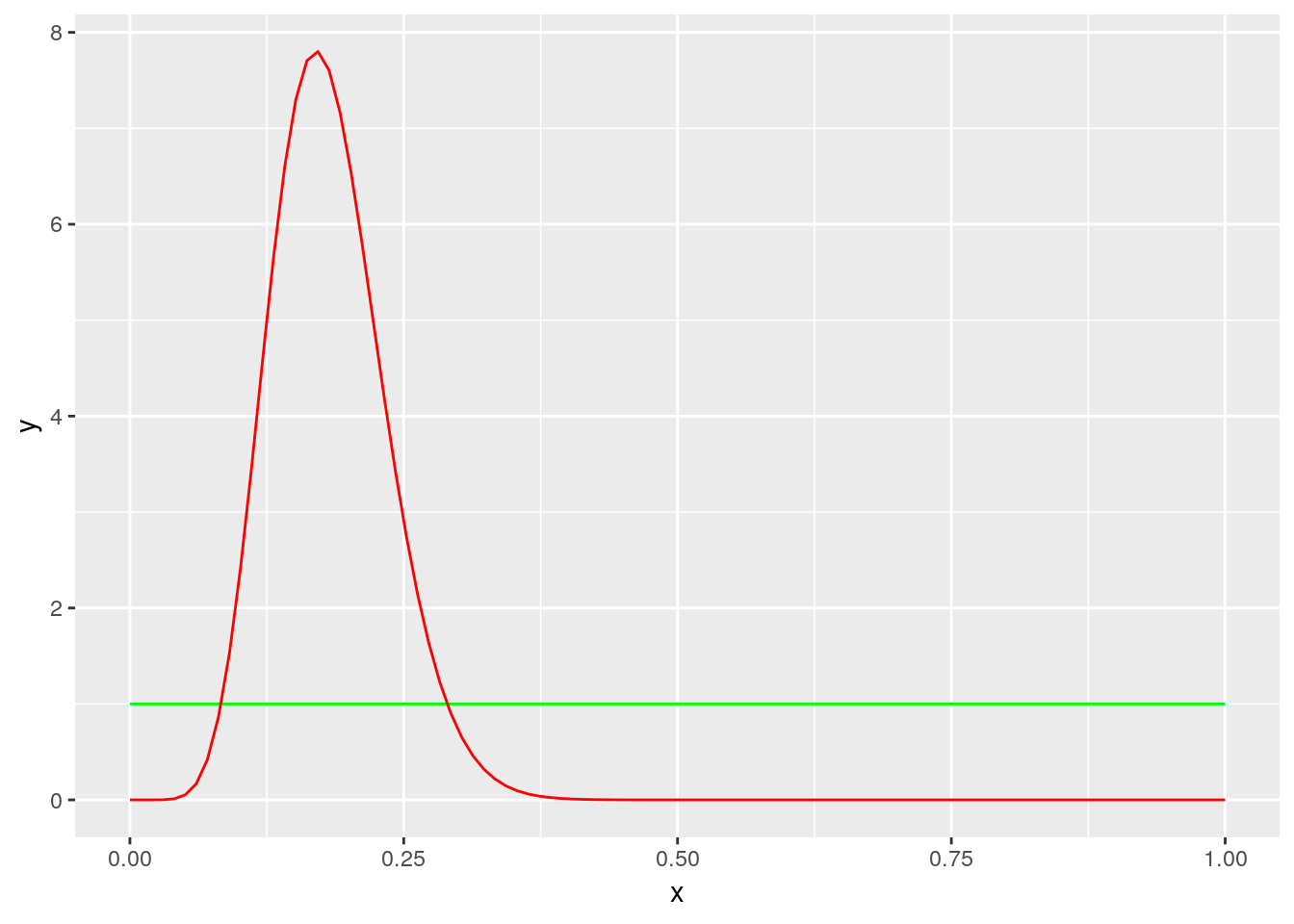
Implementing a MCMC algorithm
Compute the likelihood for a given value of \(p\)
binom_loglikelihood<- function(y, p, m){
dbinom(x = y, size=m, prob = p)
}
binom_loglikelihood(y=YM, p=0.1, m=m)## [1] 0.04297662binom_loglikelihood(y=YM, p=0.2, m=m)## [1] 0.1235354A function to update the current parameter value
rprop <- function(p.courant, sd.explore=0.1){
p.courant + sd.explore*rnorm(1)
}
dprop <- function(p.courant, p.propose, sd.explore=0.1){
dnorm(p.courant-p.propose, sd=sd.explore)
}Metropolis Hastings ratio
ratio <- function(p.courant, p.propose, sd.explore){
if(p.propose>1 || p.propose <0 ){
rat <- 0
} else
{
rat <- (binom_loglikelihood(YM, p.propose, m=m) * dbeta(p.propose, s1, s2)) / (binom_loglikelihood(YM, p.courant, m=m) * dbeta(p.courant, s1, s2))*(dprop(p.propose, p.courant, sd.explore) / dprop(p.courant, p.propose, sd.explore))
}
return(rat)
}Metropolis Hastings algorithm
p.init <- 0.8
n.iter <- 500
sd.tune <- 0.1
p.post <- rep(NA, n.iter)
p.courant <- p.init
for (i in 1 : n.iter){
p.cand <- rprop(p.courant, sd.explore = sd.tune)
rat <- ratio(p.courant, p.cand, sd.tune)
if(runif(1)<rat){
p.post[i] <- p.courant <- p.cand
} else {
p.post[i] <- p.courant
}
}
df.post <- data.frame(p.post=p.post, niter=1:n.iter)
p <- ggplot(data = df.post, aes(x=niter, y=p.post)) + geom_point()
p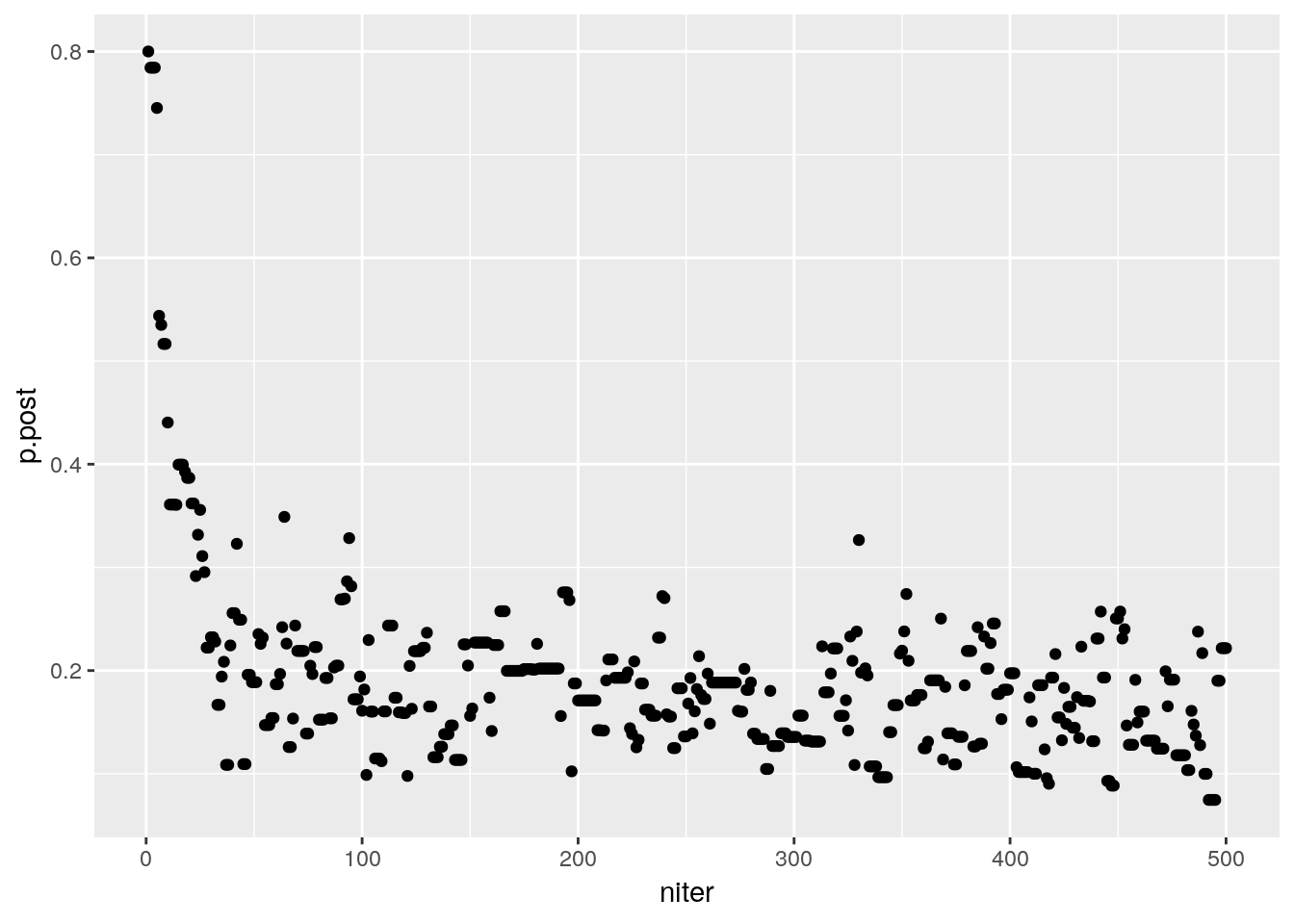
p <- ggplot(data = df.post, aes(x=p.post)) + geom_histogram(aes(y=..density..)) + xlim(c(0,1)) +stat_function(aes(x = p.post, y = ..y..), fun = dbeta, colour="green", n = 100,
args = list(shape1 = s1, shape2 = s2)) + stat_function(aes(x = p.post, y = ..y..), fun = dbeta, colour="red", n = 100,
args = list(shape1 = YM+s1, shape2 = m-YM+s2))
p## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.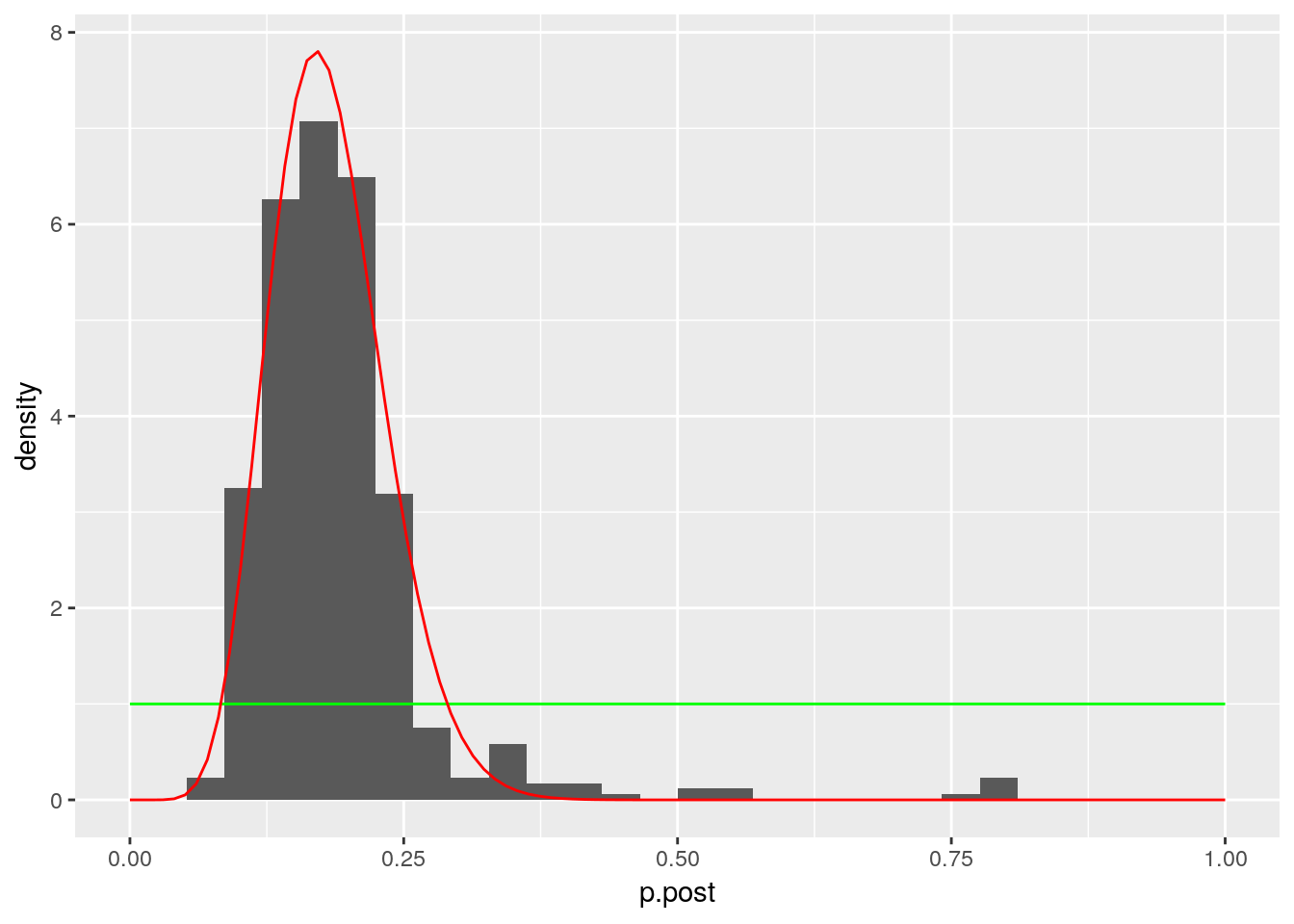
Captures successives sans remise
Problématique et modélisation
La méthode d’inventaire de DeLury (DeLury,1947) consiste à effectuer un certain nombre de pêches successives pour évaluer la taille d’une population inconnue \(\nu\) à l’aide d’un dispositif de capture (le plus souvent pêche électrique) d’efficacité \(\pi\) . L’efficacité \(\pi\) est la probabilité de capture d’un individu: elle dépend du milieu et de l’effort de pêche, et peut dépendre de la taille de l’individu. Les poissons capturés à chaque pêche ne sont ni marqués, ni remis à l’eau.
On appelle \(m\) ce nombre de pêches successives et \(C_{1}, C_{2}, \ldots, C_{i},\ldots,C_{m}\) les quantités capturées successivement obtenues.
- A l’aide de la loi binomiale, proposer un modèle simple d’échantillonnage de \(C_{1},C_{2},\ldots,C_{i},\ldots,C_{m}\) et en dessiner le graphe acyclique orienté (DAG).
- Exprimer les hypothèses qui sous-tendent votre modélisation.
- Dire quelles sont les observables et quels sont les paramètres.
- Ecrire un programme de simulation sous \(R\) qui simule un enlèvement de \(m=4\) pêches d’une population de poissons.
On pourra prendre \(\nu=50\) et \(\pi=\frac{1}{4}\) pour fixer les idées.
Estimation par méthode bayésienne
Montrer qu’une loi béta de paramètres \(a=1,\) \(b=3\) est une loi a priori très acceptable pour encoder le jugement d’un expert en dispositif de pêche électrique annonçant que sa meilleure évaluation personnelle pour \(\pi\) est de l’ordre de \(\frac{1}{4}\) \(\ \) et qu’il est prêt à parier \(50\%/50\%\) environ sur l’intervalle \([0.1,0.4].\)
- Simuler les résultats un enlèvement de \(m=4\ \)pêches d’une population de poissons avec \(\nu=50\) et \(\pi=\frac{1}{4}\) pour créer un jeu de données.
- Ecrire un programme avec appel à WinBUGS (ou jags) pour réaliser l’inférence du modèle après avoir choisi un prior peu informatif pour \(\nu\).
- Le faire tourner sur données simulées et vérifier la bonne qualité de l’encadrement réalisé par la loi a posteriori des “inconnues”.
- On pourra choisir quelques valeurs types du triplet génératif (\(m,\nu,\pi\)) pour illustrer sur des jeux de données différents le fonctionnement de cette inférence bayésienne.
- Appliquer votre méthode bayésienne sur les deux jeux de données d’anguilles et vairons du Couesnon, (données tirées d’une enquête de Beaudouin et Pontini (1973) et reprises dans le tableau suivant), discuter des résultats (en imaginant que vous ayez acces aux données en deux temps : d’abord seulement les deux premières pêches, puis ensuite les trois pêches) et traduire les résultats de cette approche en recommandations à l’intention des gestionnaires du cours d’eau:
| Espèces | Peche1 | Peche2 | Peche3 |
|---|---|---|---|
| Anguilles | 28 | 11 | 4 |
| Vairons | 60 | 54 | 58 |
Bibliographie
- Beaudouin P., Pontini G., 1973. étude hydrobiologique du bassin du Couesnon. Diplôme d’Agronomie approfondie, E. N . S. A., Rennes.
- DeLury D.B.,1947. On the estimation of biological populations. Biometrics, 3(4) , 145-167.
TD estimation de la taille d’une poulation d’otaries
L’objectif du TD est d’estimer la taille d’une population d’otaries sur l’ile Marion en Antarctique.
Un extrait de la publication présentant les données et le problème est disponible ici.
Nous nous appuierons sur 3 jeux de données qui sont
- les expériences de capture marquage recapture CMR_Data
- les comptages directs DC_Data
- Les comptages depuis la falaise Cliff_data
TD estimation de l’évolution du stock de merlu en Namibie
L’objectif de deuxième TD est d’estimer l’évolution du stock de merlus de Namibie entre 1964 et 1988.
La publication présentant les données et le problème de l’évaluation de stochk est disponible ici.
Les données donnent
- les captures en millier de tonnes,
- Un indice d’abondance relatif (CPUE) exprimé en tonnes par heure de chalutage.
Quelques idées sur un modèle de dynamique de stocks
Un modèle assez classique de dynamique de population, nommé modèle de production de biommasse, est donné par la formule suivante : \[B_{t+1} = B_t + r B_{t} \left ( 1- \frac{B_t}{K}\right) - C_t\] Expliquer pourquoi une gestion soutenable est caractérisée par une population telle que \[ C_{t}= r B_{t} \left ( 1 - \frac{B_t}{K} \right).\]
Cette fonction à la forme suivante 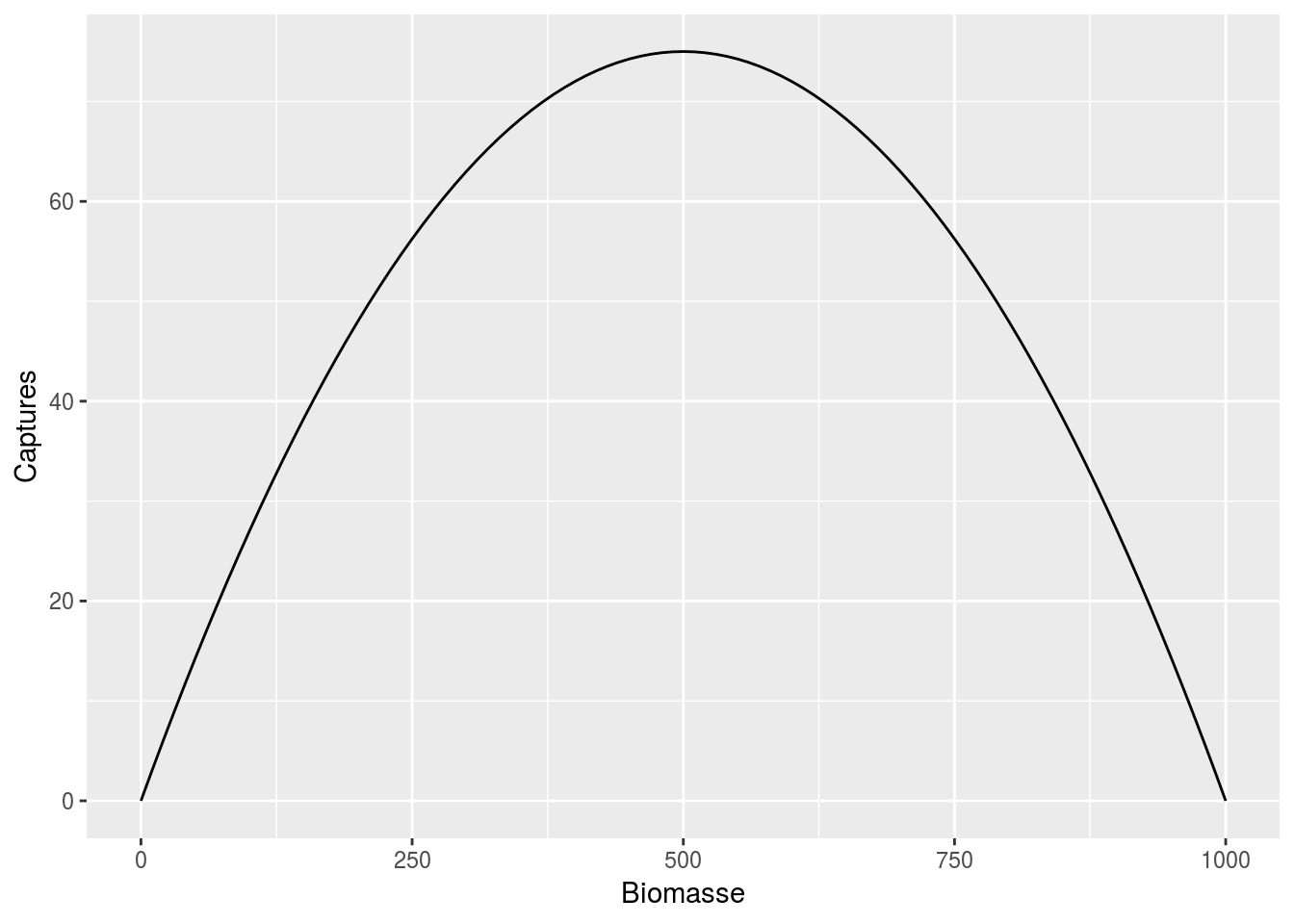
On appelle capture maximale durable \(C_{MSY}\) la quantité \(rK/4\), expliquer ce que représente cette quantité.
Dans le cadre d’une gestion durable de la pêche on essaie au plus possible de s’approcher de la biommasse correspondant à cette valeur de référence. Pour cela il faut être capable d’estimer \(r\) et \(K\).
Simulation d’un modèle de production de biomasse
On se fixe \(K=1000\) et \(r=0.3\), simuler un modèle de dynamique d’une population non exploitée.
Ce modèle est une simplification, on va donc y ajouter une part de stochasticité pour tenir compte de l’approximation de notre processus.
On définit maintenant \[B_{t+1} = \left \lbrace B_t + r B_{t} \left ( 1- \frac{B_t}{K}\right) \right \rbrace e^{E_t} - C_t,\] où \(E_t\) est un bruit gaussien \(\mathcal{N}(0,\sigma^2_P)\).
Refaire la simulation avec \(\sigma_P=0.5\), \(\sigma_P=1\), \(\sigma_P=2\).
Bien sûr dans un contexte réelle, \(B_t\) n’est jamais connue. Par contre, on peut avoir accès à un indice d’abondance \(I_t\). On suppose que \[I_t = q \, B_t \, e^{O_t},\] où \(O_t\) est un bruit gaussien \(\mathcal{N}(0,\sigma_O^2)\).
Nstep <- 30
B <- numeric( Nstep)
K <- 1000
r <- 0.3
sigma_P <- 0.01
q <- 0.1
sigma_O <- 0.01
B[1] <- .9 * K
E <- rnorm(Nstep,sd = sigma_P)
O <- rnorm(Nstep,sd = sigma_O)
for(i in 1:(Nstep - 1)){
B[i+1] <- (B[i] + r * B[i] * (1 - B[i]/K)) * exp(E[i])
}
data.frame(time = 1:Nstep, B = B, I = q * B * exp(O)) -> stock
ggplot() + geom_line(data = stock, aes(x=time, y=B)) +
xlab('Annee') + ylab('Biomass') +
geom_point(data = stock, aes(x=time, y=I / q), col = 'red') + ggtitle('Les variables cachées et observées')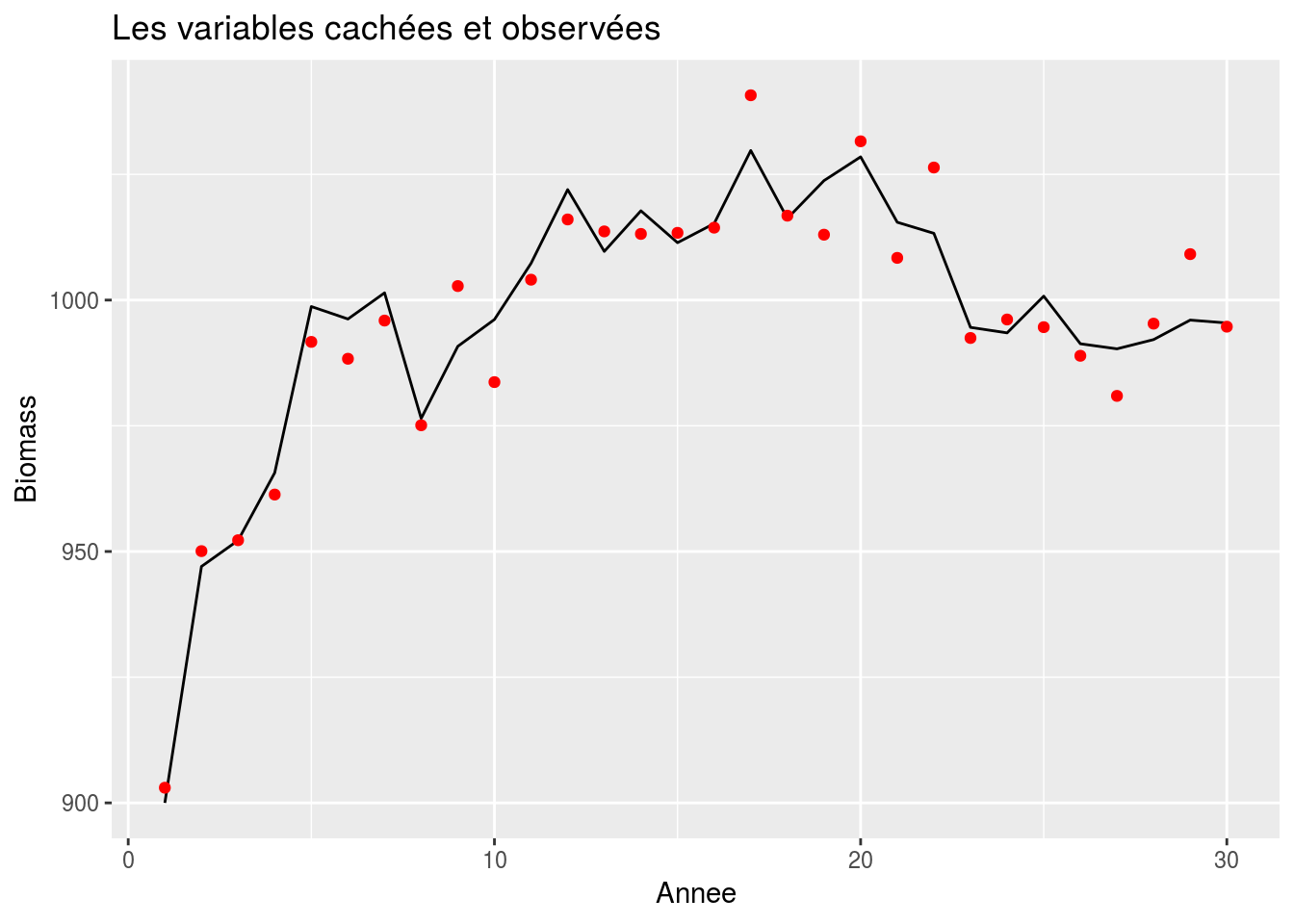
ggplot() +
xlab('Annee') + ylab('Biomass') +
geom_point(data = stock, aes(x=time, y=I / q), col = 'red') + ggtitle('Les variables observées')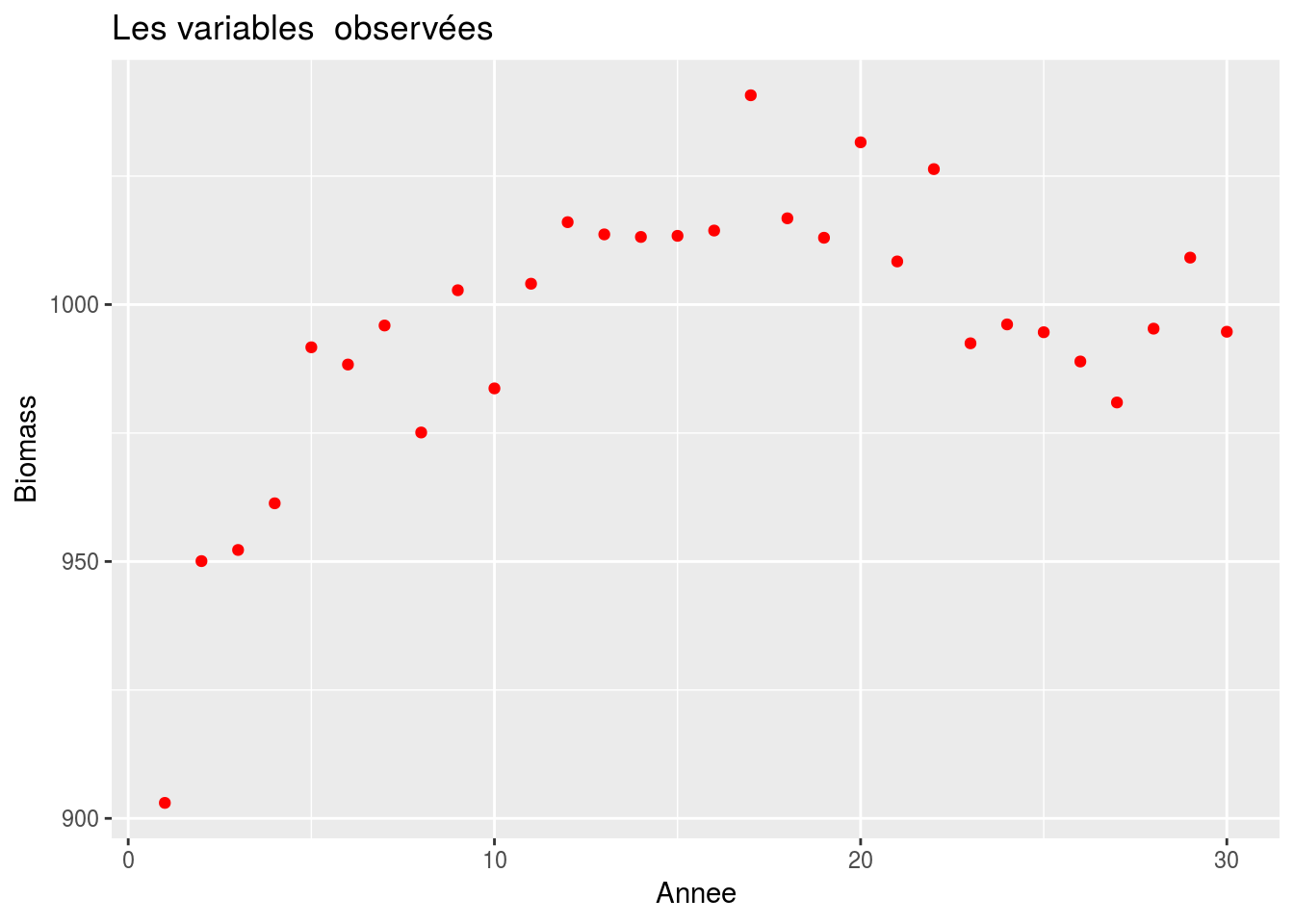
Le but à partir des observations d’indices d’abondance, on veut reconstruire la chronique des biomasses.