Variabilité d’échantillonnage
Qu’attend on d’un bon échantillonnage ?
Différentes stratégies d’échantillonnage
Echantillonnage aléatoire simple (EAS)
Présentation
Définition L’EAS consiste à prélever (sans remise) n éléments dans une population de taille N, au hasard et de façon indépendante. Chaque élément possède la même probabilité d’être échantillonné et chacun des échantillons possibles de taille n possède la même probabilité d’être constitué.
Exemple
On s’intéresse aux captures dans une population de \(N=36\) pêcheurs. On choisit au hasard 18 pêcheurs, soit un effort d’échantillonnage \(f=0.5\).
Echantillonnage Débarquement - cours E. Rivot
N <- 36
n <- 18
pecheur_echant <- sample(1:N, size = n, replace =FALSE)Propriétés de l’estimateur de la moyenne
Chaque individu a la même probabilité d’être dans l’échantillon. par exemple pour l’individu \(i=5\).
Expliquer le code suivant :
i <- 5
res <- replicate(400, i %in% sample(1:N, size= n, replace = FALSE))
sum(res) / length(res)## [1] 0.4775L’estimateur de la moyenne est ${X}n={i=1}^n{X_i}, $ et l’estimateur de la variance est \(S^2 =\frac{1}{n-1} \sum_{i=1}^n(X_i -\bar{X}_n)^2\).
Alors \[Var(\bar{X}_n)= (1-f) \frac{\hat{\sigma}^2}{n}\]
La variance vient du fait qu’on n’échantillonne pas complètement la population.
- Que se passe t il si \(n\to N\) ?
- Que peut-on dire de \(f\) si la population est très grande ?
Propriétés de l’estimateur de la somme
L’estimateur de la somme est ${X}n^+= {i=1}^n {X_i} = N {X}_n, $ Alors \[Var({X}_n^+)= \frac{N^2}{n} (1-f) {\hat{\sigma}^2}\]
- Que se passe t il si \(n\to N\) ?
Exemple : Estimation de la population totale de poissons
Sur une zone de 10 km\(^2\), 30 traits de chalut sont réalisés.
Chacun balaie une surface de 20m x 5000m = 100 000 m\(^2\) = 1/10 de km\(^2\) soit 1/100 de la surface totale.
- Que vaut \(f\) ?
- Estimer la population totale à partir de l’estimation de la population moyenne par traits de chalut ?
Données : \(\bar{x} = 1000\),\(\hat{\sigma}^2 = 10000,\)
Optimisation de la taille de l’échantillon
Il est souhaitable d’avoir une bonne précision mais pas à n’importe quel prix !! et l’échantillonnage coute cher !
Si on veut une précision de 10\(\%\) quelle taille d’echantillon faut-il choisir ?
Le coefficient de variation est défini par \[CV_{\bar{X}_n} =\frac{\sqrt{Var(\bar{X}_n)}}{E(\bar{X}_n)}\] En déduire la valeur de \(n\) minimale pour avoir un CV estimé de 10\(\%\).
Exercice sur la relation age - taille
## age length sexe site
## Min. : 1.00 Min. :12.73 f:292 Site1:181
## 1st Qu.: 6.00 1st Qu.:22.72 m:208 Site2:319
## Median :11.00 Median :26.51
## Mean :13.78 Mean :26.19
## 3rd Qu.:20.00 3rd Qu.:29.68
## Max. :40.00 Max. :40.32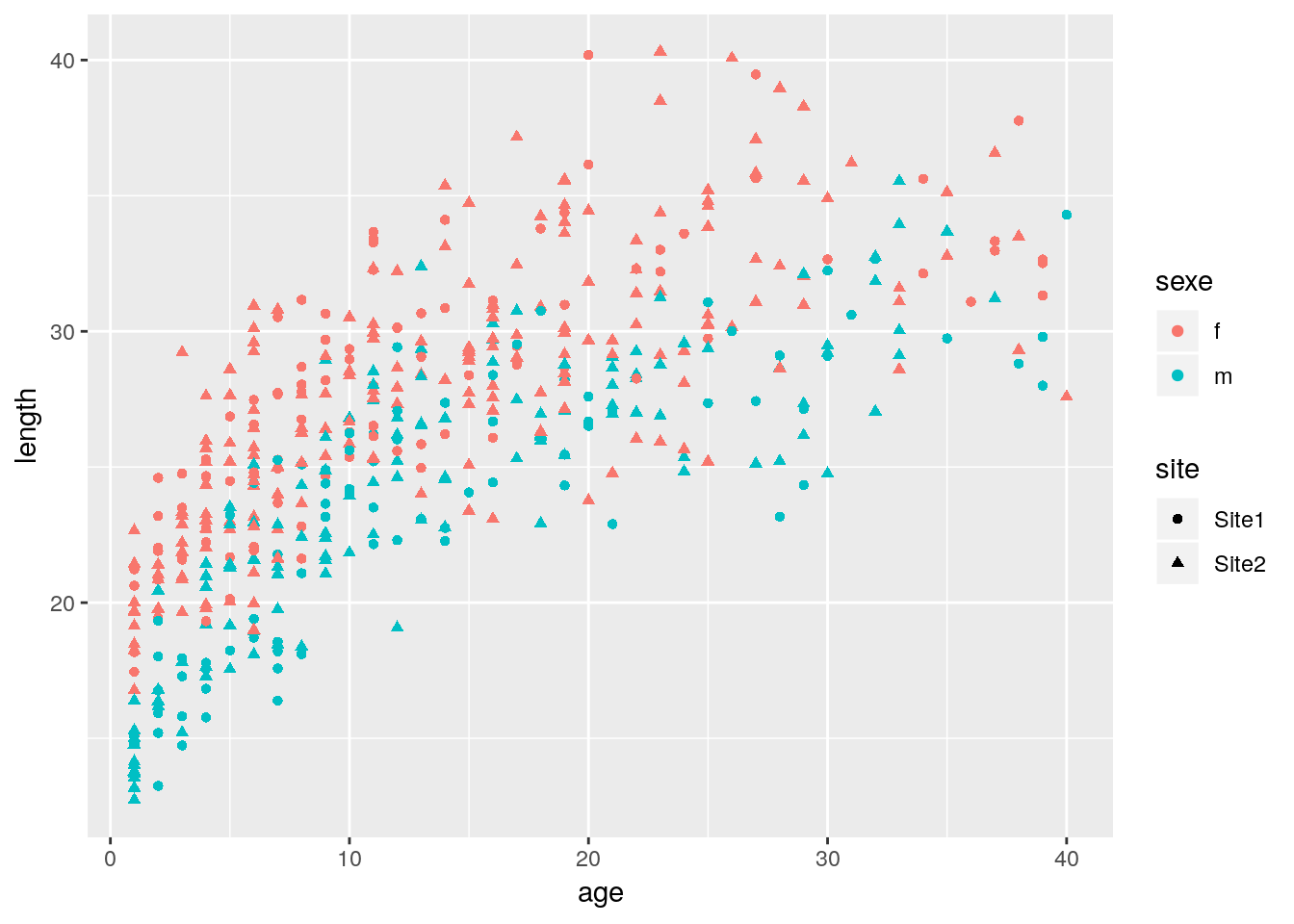
Supposons que le jeu de données large_growth_data contient l’ensemble d’une population d’intérêt.
Echantillonner avec \(f = 0.2\) et estimer la taille moyenne.
Repliquer cette opération plusieurs fois et représenter la loi de l’estimateur de la moyenne ainsi que la vraie valeur.
load('data/large_growthdataset.Rdata')
N <- nrow(large_growth_data)
f <- 0.2
n <- round( f * N )
L <- 100
estimates_EAS <-replicate(L, {
echant <- sample(1 : N, size = n, replace = FALSE)
dplyr::slice(large_growth_data, echant) %>% dplyr::select(length) %>% colMeans()
}) %>% as.data.frame() %>% select(mean = '.')
ggplot(estimates_EAS, aes(x=mean)) + geom_histogram(fill = 'darkgreen', alpha = 0.6, bins = 10) +
geom_vline(xintercept = mean(large_growth_data$length)) + xlim(c(24, 28))## Warning: Removed 1 rows containing missing values (geom_bar).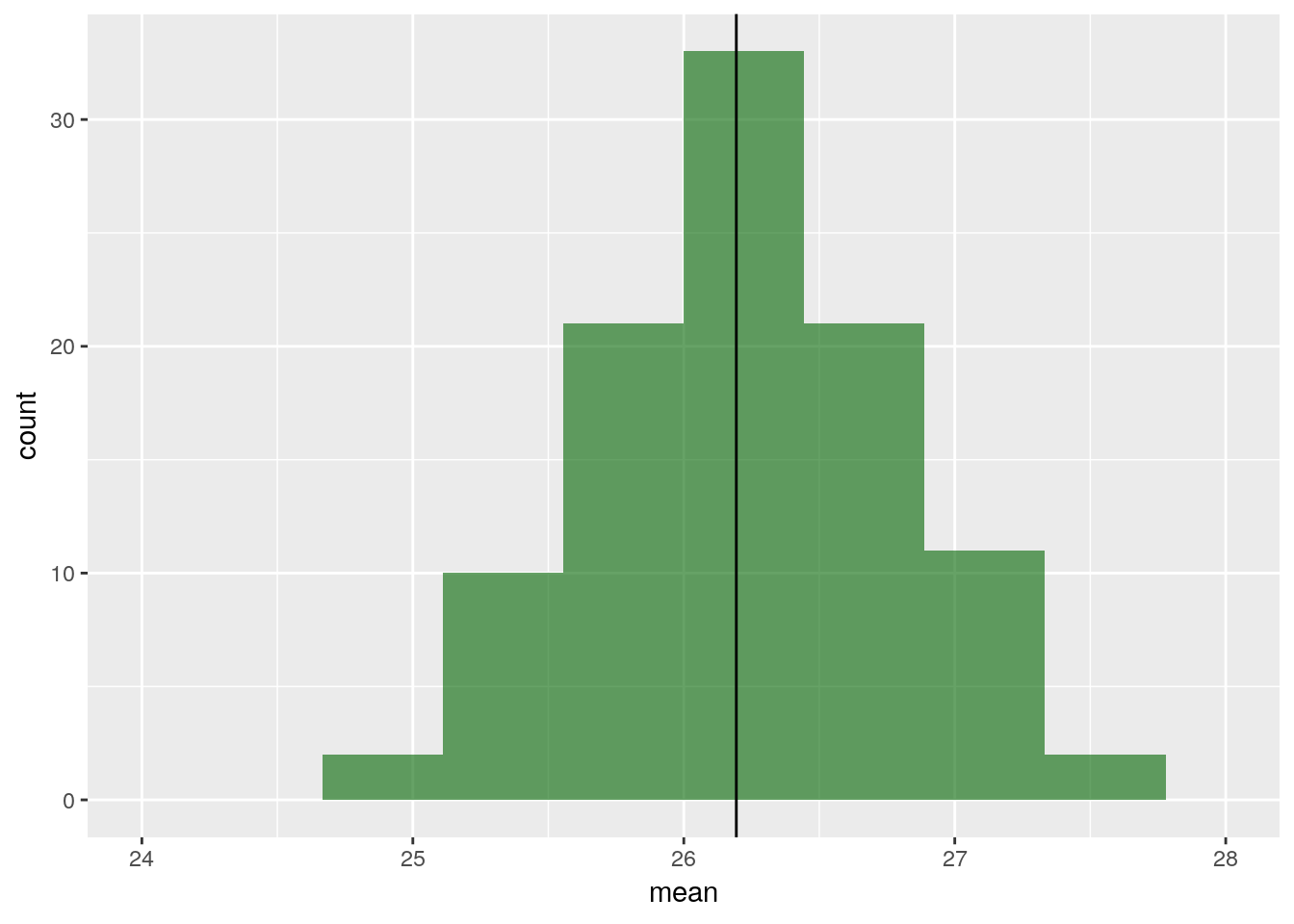
La variance de l’estimateur calculé sur 100 réalisations vaut 0.5443348.
Intérêts et limites
- L’échantillonnage est simple (quoique ….)
Les propriétés des estimateurs sont sympathiques
peu efficace pour estimer des différences au sein d’une population,
Echantillonnage stratifié (ES)
Présentation
L’échantillonnage stratifié à subdiviser une population hétérogène en sous populations ou « strates » plus homogènes, mutuellement exclusives et collectivement exhaustives.
La population hétérogène de taille N est ainsi divisée en S strates (\(s = 1,\ldots, S\)) plus homogènes d’effectif \(N_s\) telles que \(N = \sum_{s=1}^{S}N_s\).
Un échantillon est prélevé dans chacune des strates en appliquant un plan d’échantillonnage. La solution la plus simple et la plus classique est d’appliquer un EAS dans chaque strate (mais on peut appliquer un autre plan).
Propriétes
La variance provient uniquement de l’échantillonnage intre strate, pas de variance d’estimation inter strate puisque toutes les strates sont vues !
Plus efficace qu’un EAS
Example
Re prendre le jeu de données large_growth_dataet proposer un échantillonnage stratifié.
Estimer la taille moyenne de la population.
- Réfléchir sur les strates pertinentes.
- Représenter la variabilité de l’estimateur.
On peut choisir de stratifier par couple (sexe x site). On imagine connu les effectifs de chaque classe et on veut échantillonner avec un taux \(f_h=0.2\) comme dans le cas de l’EAS.
Le code qui suit propose une solution utilisant largement le potentiel du package dplyr.
fh <- 0.2
strates <- large_growth_data %>%
group_by(sexe, site) %>%
summarise(no_rows = length(length))Il est possible de calculer els moyennes au sein de chaque strate et de les combiner dans une moyenne pondérée
estimated_pop_mean_1 <- large_growth_data %>%
group_by(sexe, site) %>% sample_frac(size = fh) %>% # on groupe par sexe x site et on échantillonne
group_by(sexe, site) %>% summarise(estimated_means = mean(length)) %>% # groupe par sexe x site et calcule de moyenne
inner_join(strates) %>% ungroup() %>% # concatenation avec la table strate et on degroupe
summarise( p_mean = weighted.mean(estimated_means, w=no_rows) ) # calcul de la moyenne pondérée## Joining, by = c("sexe", "site")Ou plus directement on calcule la moeyenne des individus échantillonnés
estimated_pop_mean_2 <- large_growth_data %>%
group_by(sexe, site) %>% sample_frac(size = fh) %>% # on groupe par sexe x site et on échantillonne
group_by(sexe, site) %>% ungroup() %>% summarise(p_mean = mean(length)) Pour visualiser la distribution de l’échantillonnage
estimates_ES <- data.frame( mean =
replicate(L, {
estimated_pop_mean_1 <- large_growth_data %>%
group_by(sexe, site) %>% sample_frac(size = fh) %>% dplyr::summarise(pmean = mean(length)) %>% # groupe par sexe x site et calcule de moyenne
inner_join(strates) %>% ungroup() %>% # concatenation avec la table strate et on degroupe
dplyr::summarise( p_mean = weighted.mean(pmean, w=no_rows) ) %>% # calcul de la moyenne pondérée
as.numeric()
}) )
ggplot(estimates_ES, aes(x=mean)) + geom_histogram(fill = 'darkgreen', alpha = 0.6, bins = 10) +
geom_vline(xintercept = mean(large_growth_data$length))+ xlim(c(24, 28))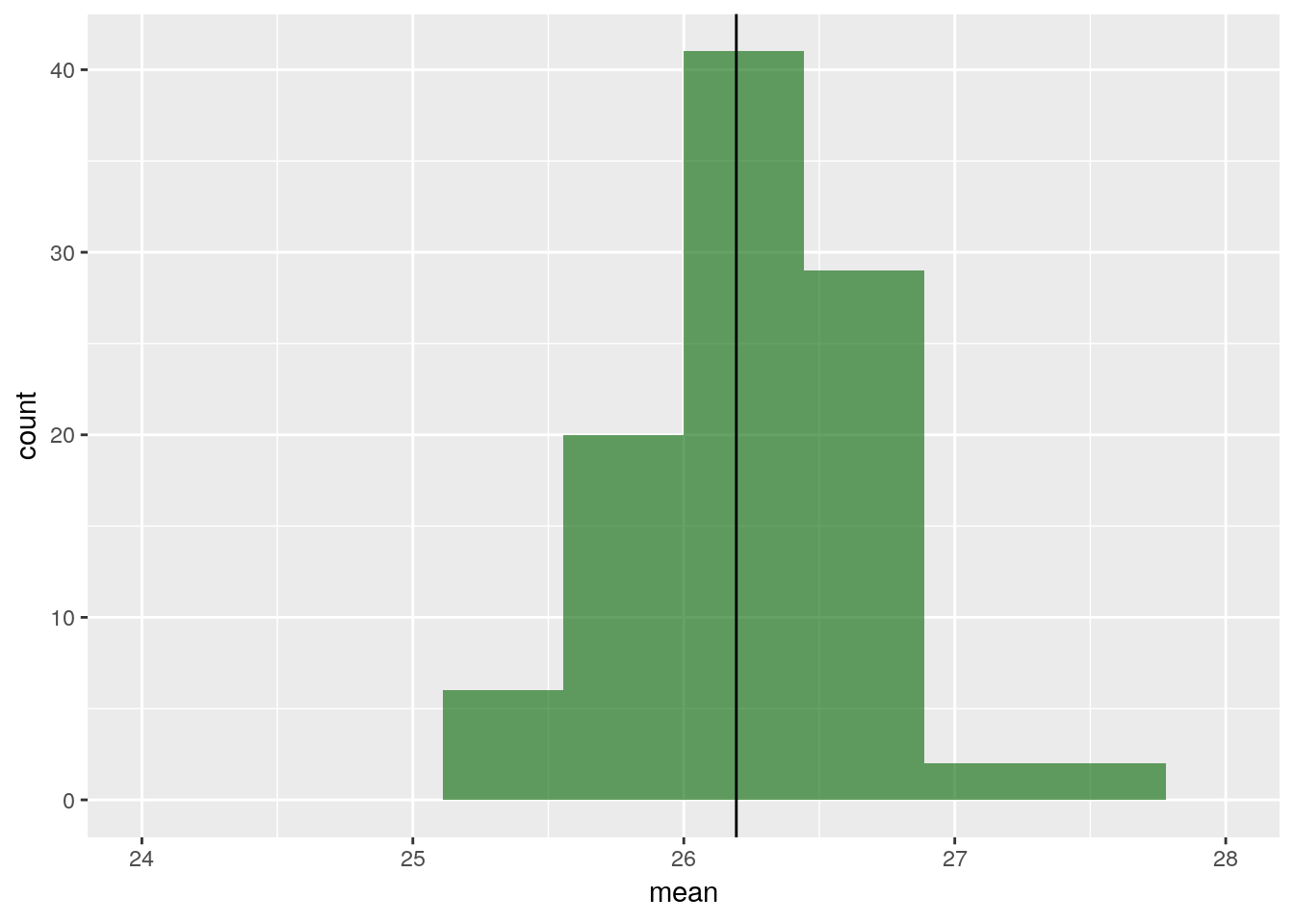
La variance de l’estimateur calculé sur 100 réalisations vaut 0.4146318.
Attention dans la réalité, on ne connait pas le poids de chaque strate.
- Que se passe t il si on se trompe dans le poids des strates ?
On va sur échantillonner une strate. Cele ci sera donc sur représentée dans l’échantillon et l’estimateur ainsi construit sera biaisé.
- Comment avoir une idée du poids des strates ?
On peut utiliser des données d’années précédentes, la littérature ou construire un EAS pour estimer le poids de chaque strate.
Intérêts et limites
L’ES est d’autant plus intéressant que : - La variance inter-strates est grande (pas de var. inter-strates dans la variance d’estimation) ; - La variance intra-strate est réduite (seule source de variance d’estimation).
A condition que les strates soient bien définies, en rapport avec la variable d’intérêt dans la population.
l’ES fournit des estimateurs sans biais et procure un gain de précision important par rapport à l’EAS.
Une erreur d’appréciation du poids des strates \(w_s\) peut entraîner un biais important dans les estimateurs de la moyenne \(\mu\) et du total \(\Sigma\).
Pour aller plus loin
A rendre pour le 24 septembre 2018
Le CCAMLR est en charge entre autre du suivi des stocks de légine en Antarctique. De nombreuses sources de données sont utilisées mais une information clé repose sur la déterminaition d’une relation de von Bertalanffy entre age et longueur.
Les individus jeunes sont plus nombreux dans la population mais l’ajustement de la courbe requiert aussi des observations sur des dinvidus plus âgés.
Décrire le protocole d’écahntillonnage utilisé dans le papier de Candy, S.G., A.J. Constable, T. Lamb and R. Williams