Variabilité d’échantillonnage
Statistique inférentielle : de l’échantillon à la population
En statistique, un objectif classique consiste à inférer des propriétés sur une population à partir d’une vision partielle de celle-ci : un échantillon
Un exemple central
Une population extra Terrestre réside sur la planète Halieutik . Cette population est inconnue des habitants de la planête Statistik mais très avancée technologiquement, les habitants d’Halieutik ont construit un vaisseau pour rendre visite à la planète Statistik. Ce vaisseau ne contient que 10 individus.
La population de Statistik ne connaît pas les motivations des habitants d’Halieutik et souhaite faire progresser sa connaissance de la morphologie sur cette nouvelle espèce (pour se préparer à toutes éventualités).
A partir des 10 individus qui descendent du vaisseau que peut-on raisonnablement affirmer sur la population générale d’Halieutik ?

C’est un problème de statistique
Plus généralement
Contrairement à ce qu’on pourrait croire, c’est un problème très classique en statistique dans tous les domaines d’applications :
- Intentions de vote de la population à partir d’un échantillon de la population,
- Evaluation du rendement de la parcelle à partir de quelques prélévements,
- Evaluation de la préférence des consommateurs à partir d’un panel,
- Evaluation de la structure des tailles de captures à partir des débarquements

Formaliser le passage de l’échantillon à la population
Il faut poser des hypothèses. Par exemple si l’on s’intéresse à la taille moyenne des habitatnts d’Halieutik.
On peut imaginer un modèle de la répartition des tailles dans la population.
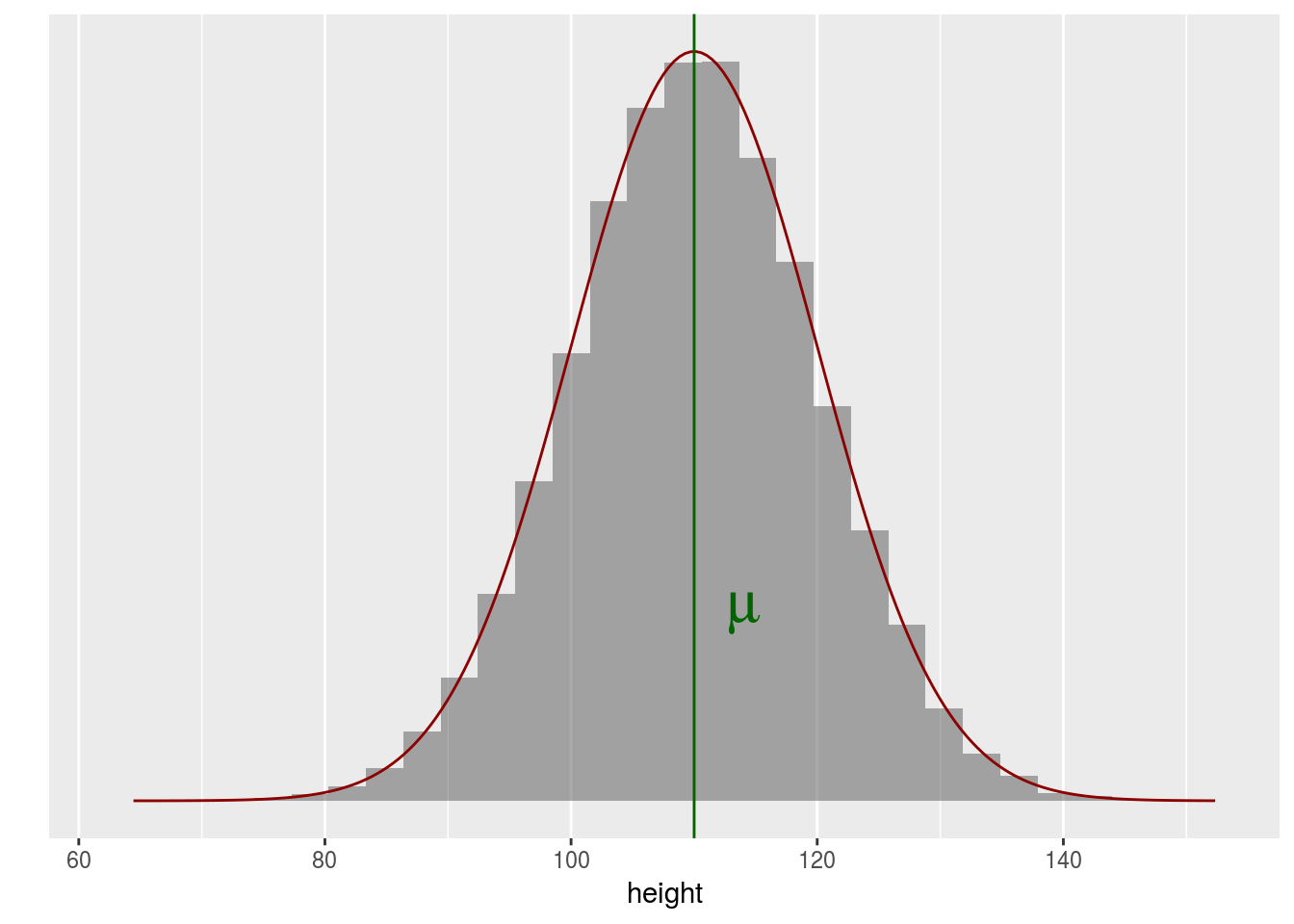
Si on choisit complètement au hasard 10 individus dans cette population quelle est la situation la plus probable ?
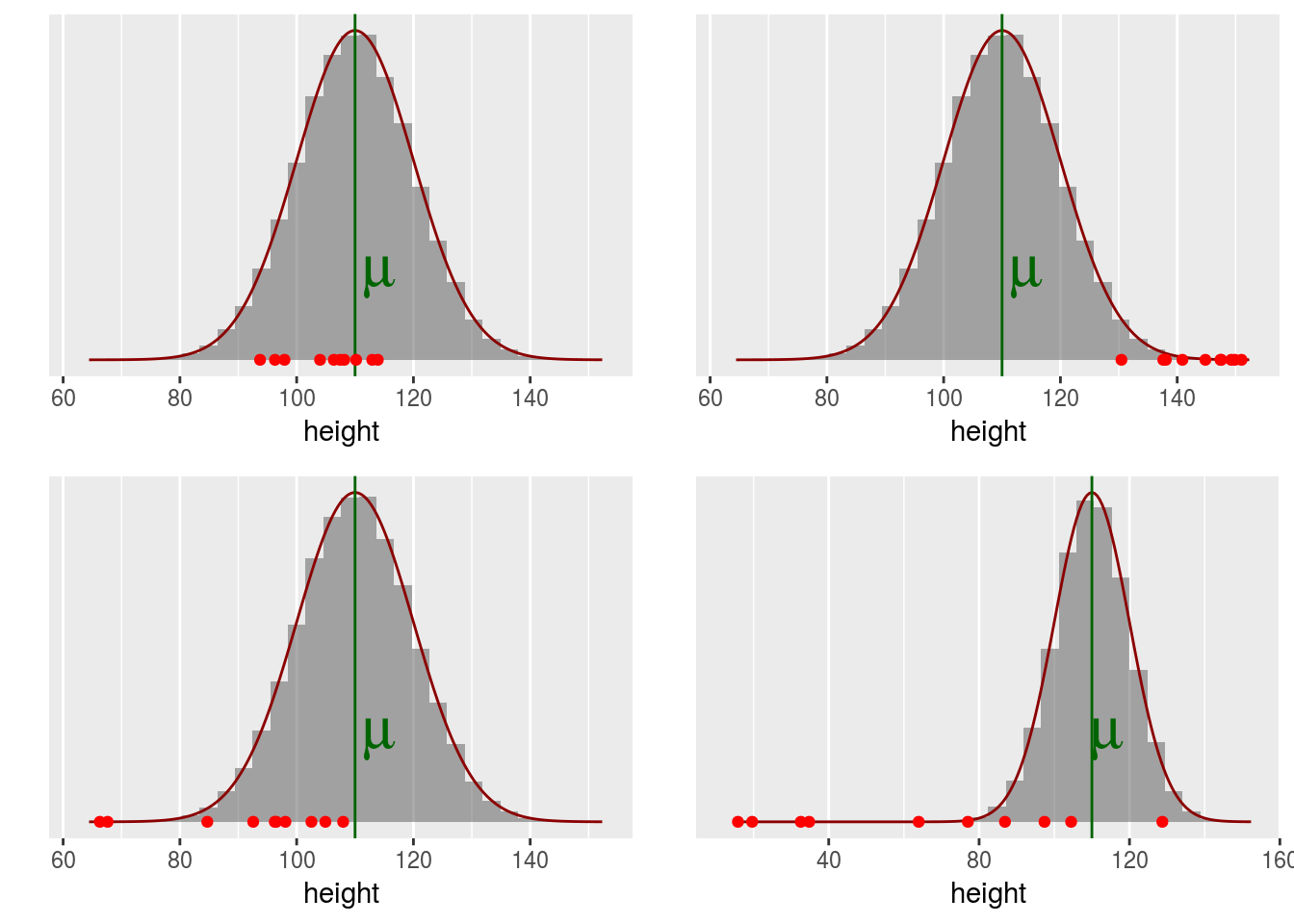
Puisque la répartition des tailles au sein de la population suit une loi normale, la taille d’un individu choisi uniformément parmi tous les individus d’une grande population suit également une loi normale. L’aléa vient du choix de l’individu parmi tous les individus possibles.
Estimateur versus Estimation
En situation réelle, on peut contrôler (un peu, cf strategie ) comment on choisit les individus au sein d’une population et à partir de notre échantillon on va chercher à construire de l’information sur \(\mu\) le paramètre qui règle la moyenne de la population.
Comment approcher \(\mu\) ?
On peut construire un estimateur : une variable aléatoire qui essaie de s’appricher de la quantité inconnue \(\mu\).
\(\mu\) désignant la moyenne de la population on peut construire la variable aléatoire, appelée moyenne empirique
\[\bar{X} = \frac{1}{n} \sum_{k=1}^{n} X_k,\] où \(X_k\) désigne la taille du k\(^{\mbox{ème}}\) individu choisi au hasard (par conséquent la taille de cette individu est bien une variable aléatoire) et \(n\)désignant la taille de l’échantillon.
Une fois qu’on a effectivement sélectionné nos individus, la taille n’est plus aléatoire, on a une réalisation de notre estimateur, c’est une estimation.
Si on s’intéresse à la taille de notre population venant d’Halieutik, l’estimateur est la moyenne empirique et sa réalisation, i.e. l’estimation la moyenne de l’échantillon.
20 vaisseaux sont arrivés sur Statistik, chacun contenant 10 individus dont on a mesuré la tailleéchantillons de taille provenant de la même population ont été relevés (data/height_sample_i.Rdata).
Construire une estimation de la taille de la population pour chaque échantillon et représenter les 20 obtenus sous forme d’histogramme.
Que constatez-vous ?
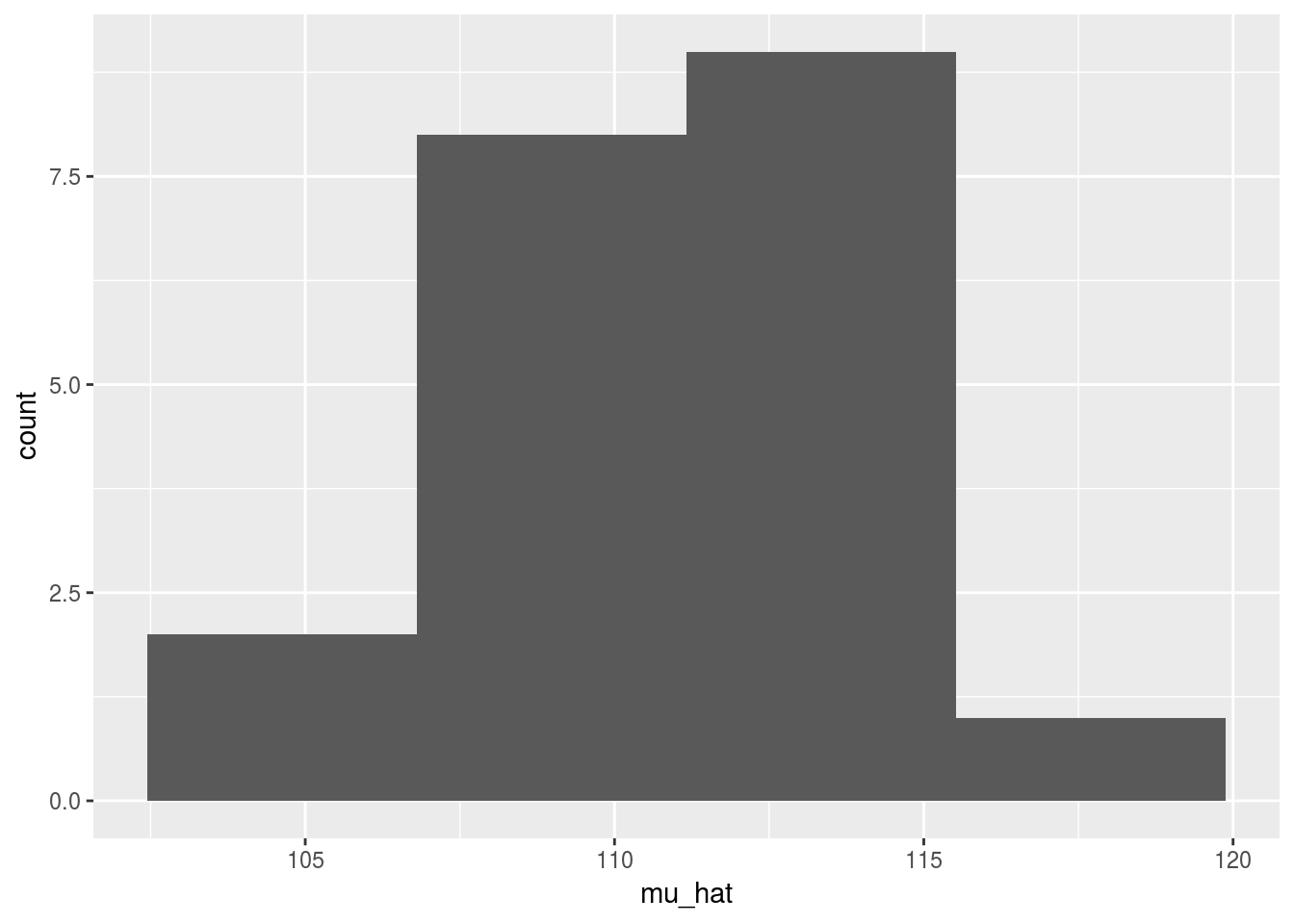
Et avec davantage d’échantillons
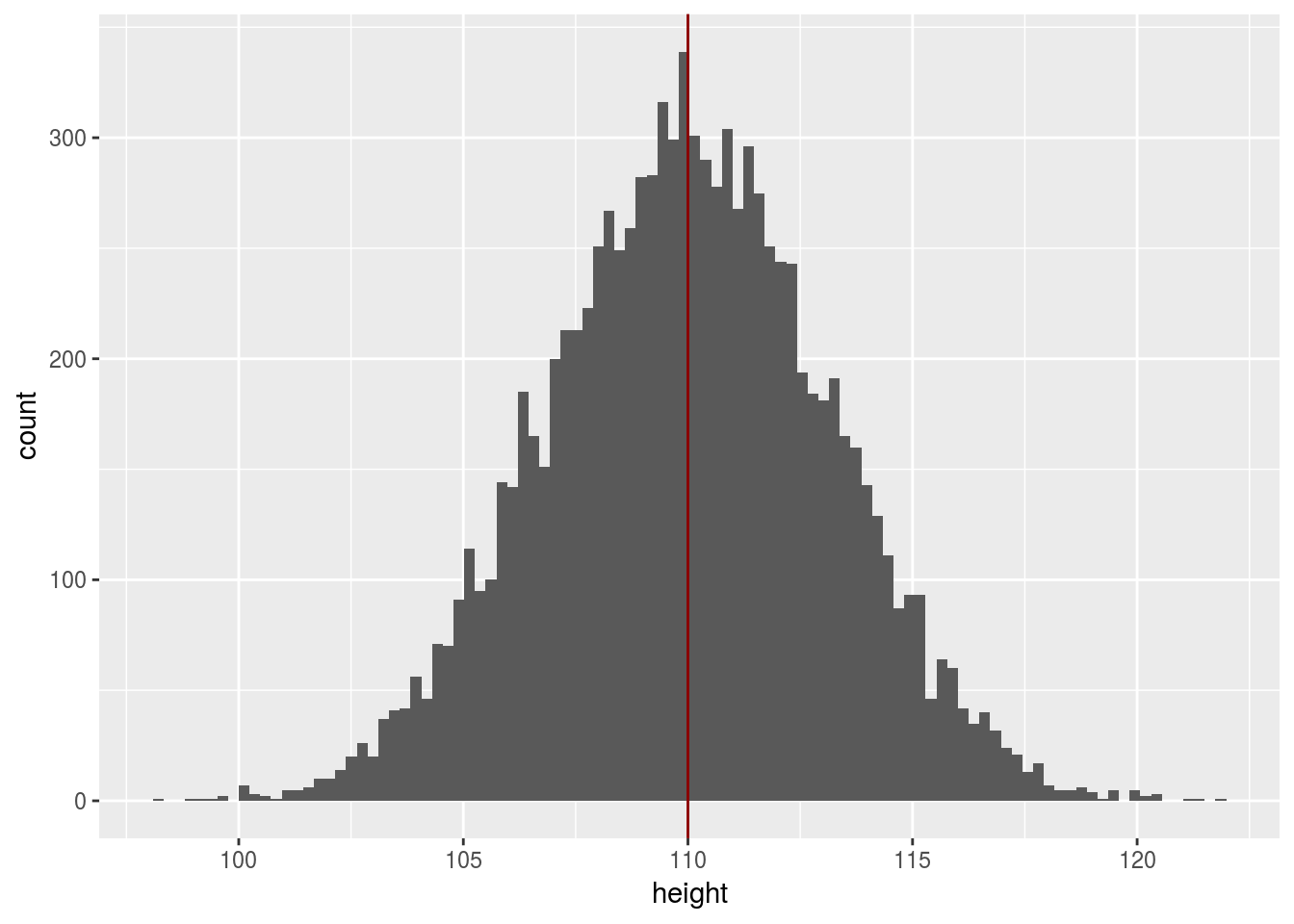
Ainsi on montre que la loi de \[\bar{X}_n \sim \mathcal{N}(\mu, \sigma^2/n)\]
Distribution des tailles dans la population
Que se passe t il si, au sein de la population la distribution des tailles ne suit pas une loi normale ?
f1 <- function(x, df, mean){
mean + dt(x-mean, df = df)
}
p2 <- ggplot(data = data.frame(height = c(mu - 20 * s, mu + 20 * s)), aes(height)) +
stat_function(fun = dgamma, n = 201, args = list( shape = mu * 0.1, rate = 0.1)) + ylab("") +
theme( axis.text.x=element_blank()) +
scale_y_continuous(breaks = NULL) +
geom_vline(xintercept = mu, col = "darkgreen")
suppressWarnings(print(p2))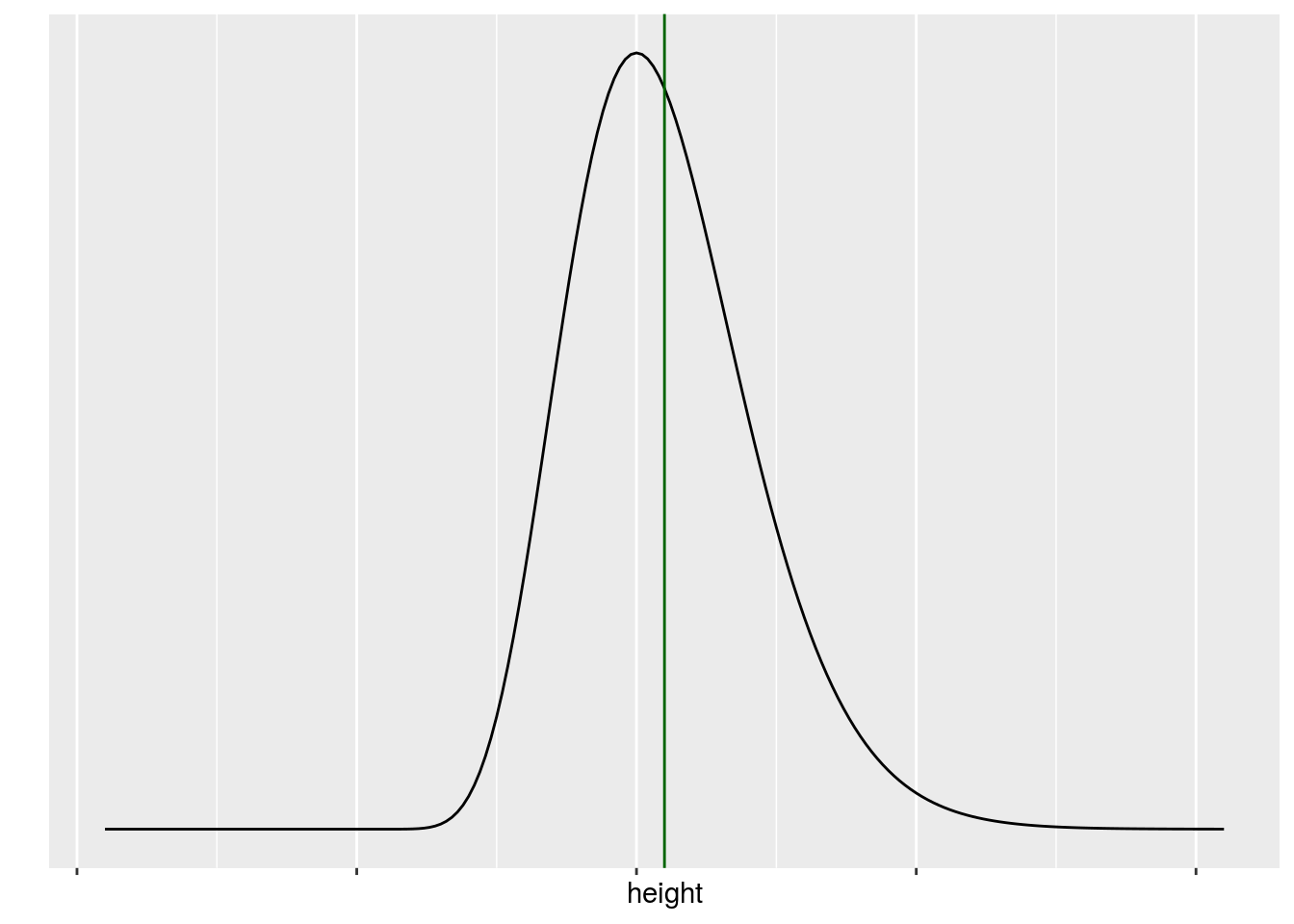
mu <- 110
n <- 20
n_dataset <- 10000
sample_gamma <- sapply(1:n_dataset, function(s_){
rgamma(n, shape = mu * 0.1, rate = 0.1)
}
)
## calcul la moyenne colonne par colonne
x <- apply(sample_gamma, 2, mean)
df1 <- data.frame(estim_mu = x)
ggplot(data = df1, aes(x=estim_mu)) + geom_histogram(bins=sqrt(n_dataset))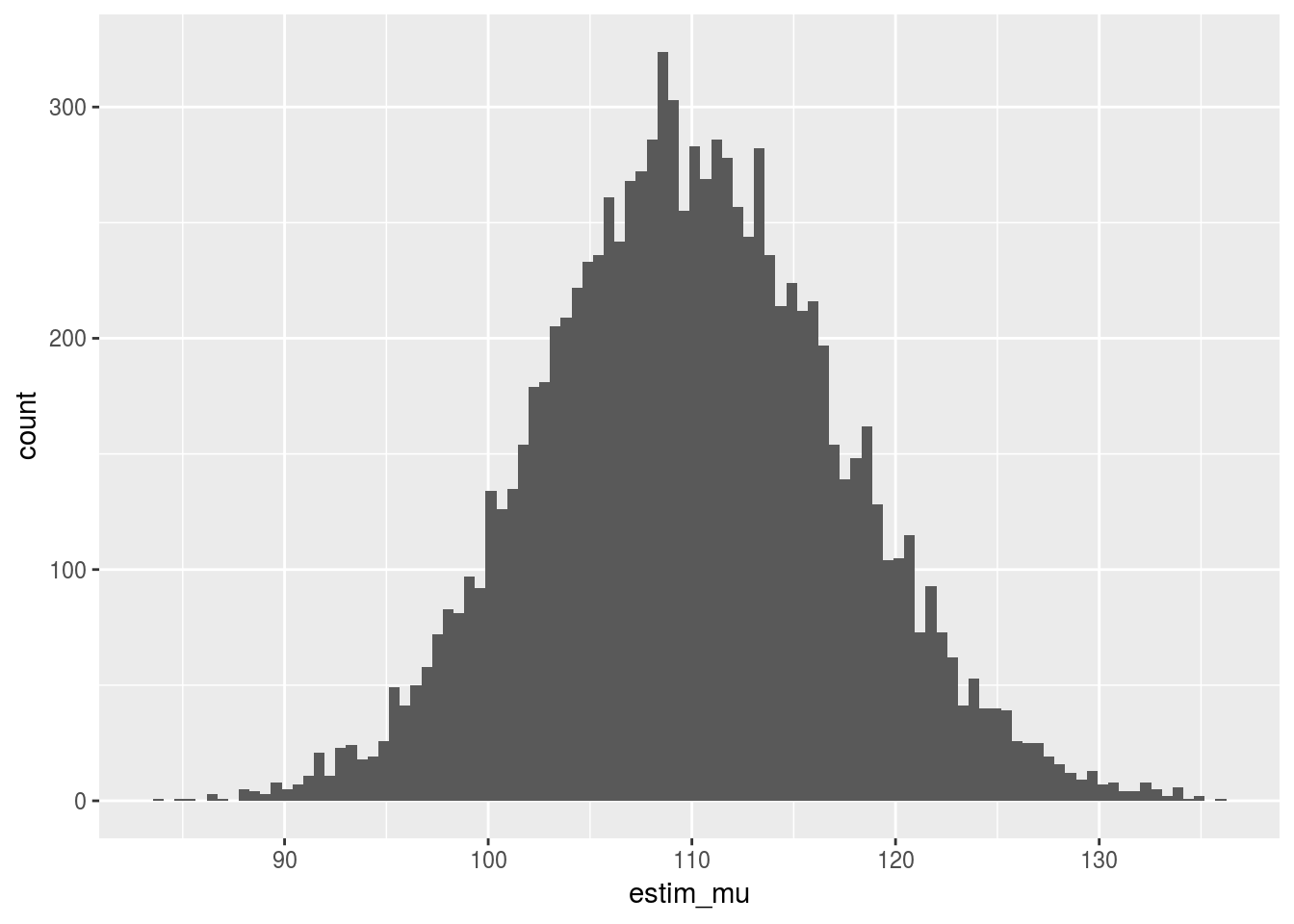
Représenter graphiquement la loi de l’estimateur de la moyenne, pour des échantillons de taille 10 et de taille 100.
Effet du choix de l’échantillon
Le vaisseau spatial est petit donc au lieu de choisir uniformément dans la population des habitants à envoyer on va privilégier les petits.
## fonction de selectivité
selectivity <- function(x, a, b){
t_x <- exp(-a * (x - b))
return(t_x / (1 + t_x))
}
## les candidats choisis preferentiellement selon leur taille
## probabilité qu'un individe de taille x soit dans l'échantillon
pref_height_sampling <- function(mean, sd, a, b){
iter_max <- 100
x_prop <- rnorm(1, mean = mean, sd = sd)
keep <- (runif(1) < selectivity(x_prop, a = a, b = b))
iter <- 1
while((!keep) & (iter <iter_max)){
iter <- iter + 1
x_prop <- rnorm(1, mean = mean, sd = sd)
keep <- (runif(1) < selectivity(x_prop, a = a, b = b))
}
if(iter >= iter_max){
cat("Nombre maximun d'itérations atteint")
return(NULL)
} else {
return(round(x_prop,2))
}
}
## echantillonner n individus
pref_n_sample <- function(n , mean, sd, a , b){
round(
sapply(1:n, function(s_){
pref_height_sampling(mean = mean, sd = sd, a = a, b = b) } ), 2)
}
## les tailles observées
height <- pref_n_sample(n, mean = mu, sd = s, a = 0.5, b = mu + 10)
mean(height)## [1] 110.8785Distribution de l’estimateur
n_dataset <- 10000
n <- 30
height_10000_rep <- sapply(1:n_dataset, function(s_){
pref_n_sample(n, mean = mu, sd = s, a = 0.5, b = mu + 10)
})
dim(height_10000_rep)## [1] 30 10000ggplot(data.frame(estim = apply(height_10000_rep, 2, mean)), aes(x = estim)) + geom_histogram(bins=sqrt(n_dataset)) + geom_vline(xintercept = mu, col = 'darkred')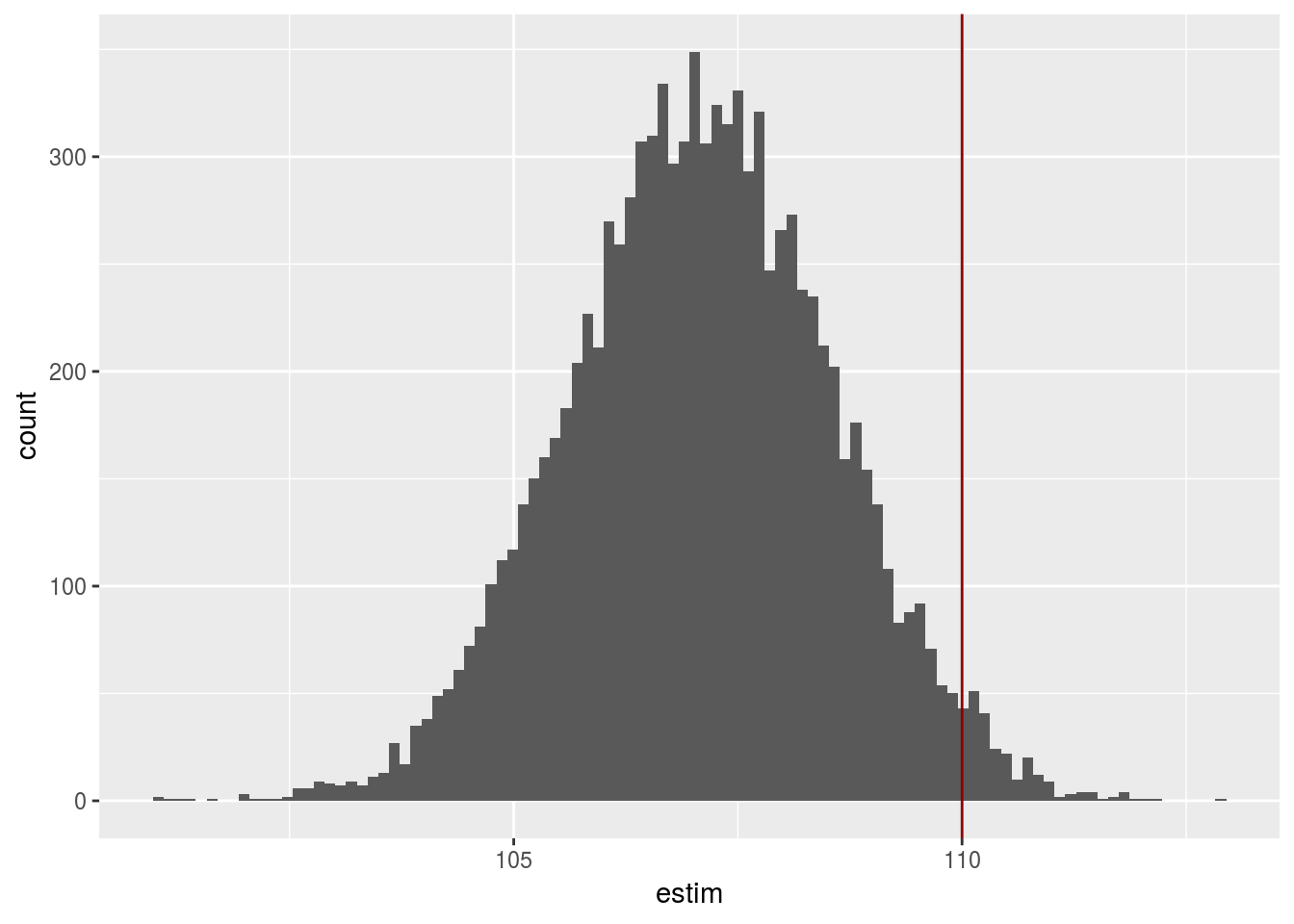
L’estimateur est biaisé.
On peut le débiaiser grâce à la théorie de l’échantillonnage et on apprendre à le faire dans le chapitre strategie pour certain type d’échantillonnage classique.
## Warning: Removed 180 rows containing non-finite values (stat_bin).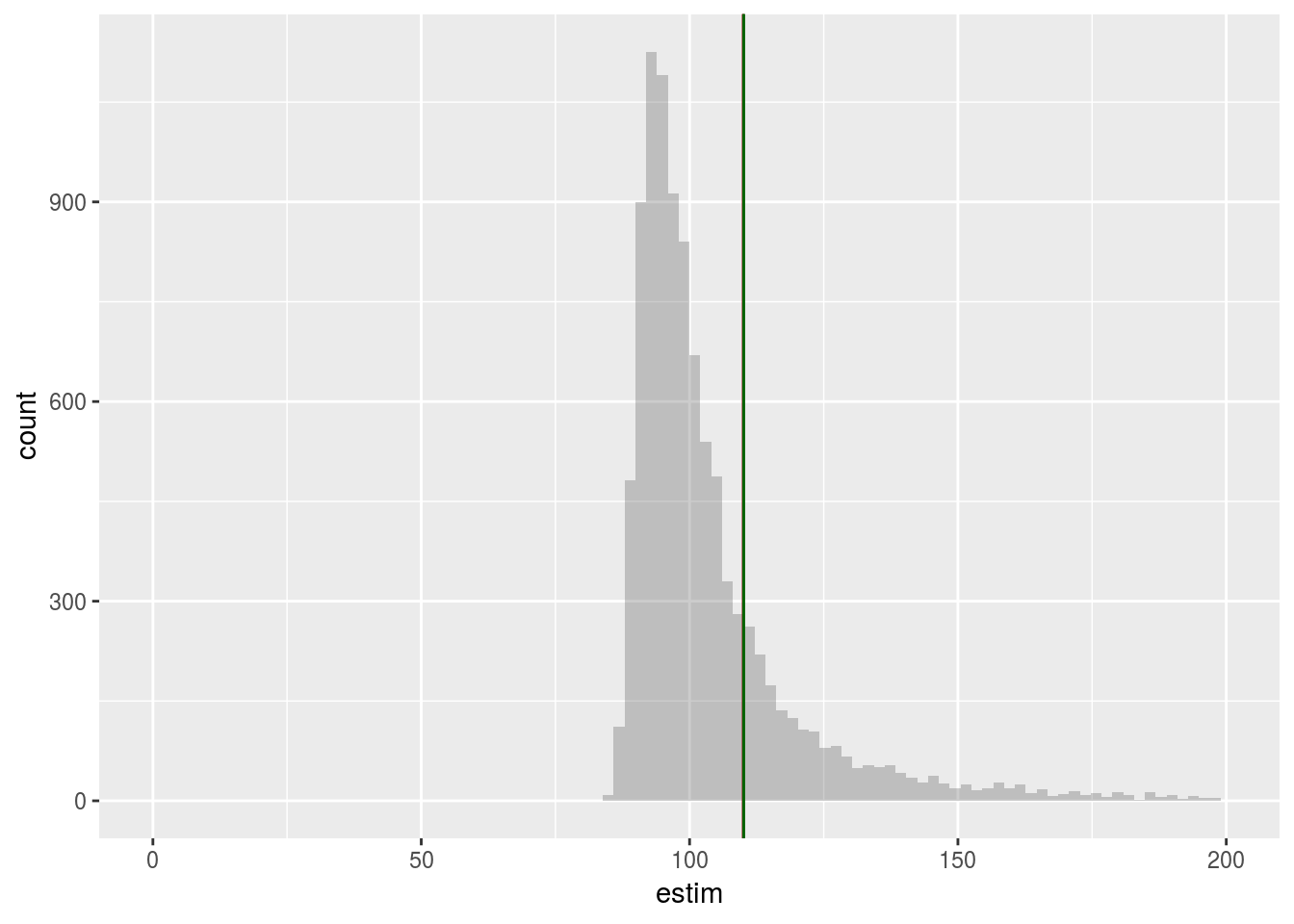
Adapter les scripts précédents pour créer un échantillonnage préférentiel crédible pour un chalut et visualiser l’effet de ce type d’échantillonnage sur l’estimation de la taille moyenne.
Intervalle de confiance
Dans le cas d’un échantillonnage uniforme, au sein d’une grande population, il est raisonnable de supposer que l’estimateur de la moyenne suit la loi suivante: \[X_n =\frac{1}{n} \sum_{k=1}^{n} X_i \sim \mathcal{N}(\mu,\sigma^2/n).\]
Graphiquement, on peut représenter les différentes quiantités de la manière suivante
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.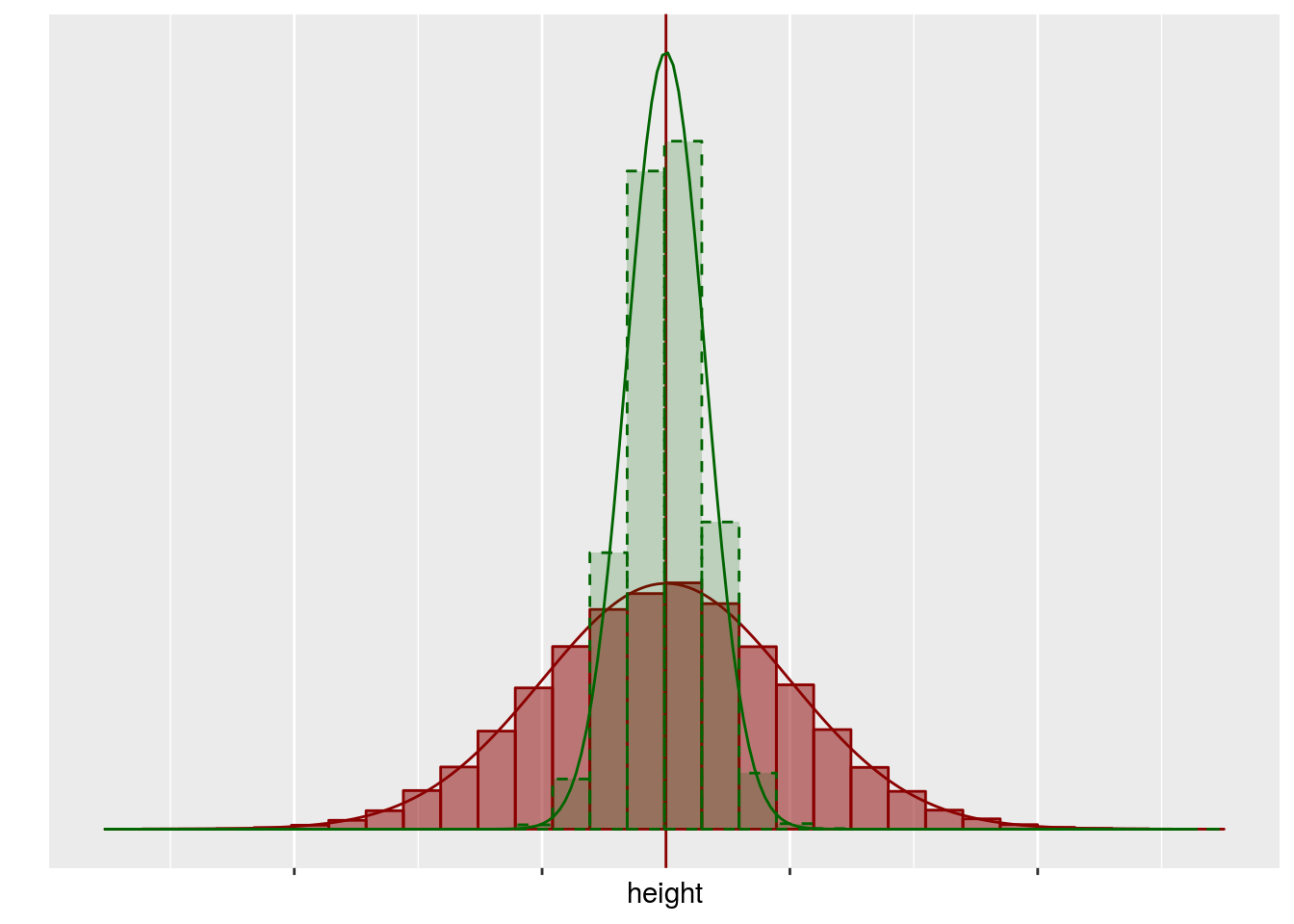
La distribution de l’estimateur est représenté en vert, la distribution des valeurs dans la population est représentée en rouge.
Dans une situation réelle, on n’a pas accès à la population, en fait tout ce qu’on peut espérer avoir est résumé dans le graphique suivant
et on veut en déduire des informations sur la population (en rouge) grâce à la distribution de l’estimateur (en vert).
Comment s’y prendre ?
- Grâce à l’échantillon on peut estimuer \(mu\) par \(\bar{x}_n\).
- Grâce à l’échantillon on peut estimuer \(\sigma\) par \(\hat{\sigma}=\sqrt{\frac{1}{n-1} \sum_{k=1}^n (x_k-} \bar{x}_n)^2\).
- On a montré que \(\bar{X}_n \sim\mathcal{N}(0,\sigma^2/n)\), mais on ne connaît pas exactement \(\sigma\). On peut construire la quantité \(T=\frac{\bar{X}_n-\bar{x}_n}{ /\hat{\sigma}}\). Cette quantité ne pédent ni de \(\mu\) ni de \(\sigma\) et on peut montrer que \[ T=\frac{\bar{X}_n-\mu}{ \hat{\sigma}/\sqrt{n}} \sim \mathcal{T}(n-1)\]
On en déduit la relation suivante
\[ P \left\lbrace \mu \in [-t_{n-1, 1-\alpha/2}\frac{\hat{\sigma}}{\sqrt{n}} + \bar{X}_n, \ t_{n-1, 1-\alpha/2}\frac{\hat{\sigma}}{\sqrt{n}} + \bar{X}_n ]\right\rbrace = 1-\alpha\] On va donc affirmer que \(\mu\) est dans l’intervalle \([-t_{n-1, 1-\alpha/2}\frac{\hat{\sigma}}{\sqrt{n}} + \bar{x}_n, \ t_{n-1, 1-\alpha/2}\frac{\hat{\sigma}}{\sqrt{n}} + \bar{x}_n ],\) avec un risque de se tromper de \(\alpha\)
On peut visualiser cette idée
n <- 10
n_dataset <- 50
alpha <- 0.05
Intervalle <- function(sample){
n <- length(sample)
x_bar <- mean(sample)
tn_1 <- qt(p = 1-alpha/2, df = n-1)
sigma_hat <- sd(sample)
c(x_bar, tn_1* sigma_hat/sqrt(n), sigma_hat)
}
int_whole <- data.frame(t(sapply(1:n_dataset, function(s_){
sample <- rnorm(n, mean = mu, sd = s)
Intervalle(sample)
})))
colnames(int_whole) <- c('x_bar', 'width', 'sigma_hat')
int_whole$y <- seq(0, 0.2, length.out = n_dataset)
ggplot(data = int_whole) + geom_errorbarh( aes( y = y, xmin = x_bar - width, xmax = x_bar + width, height = 0)) + geom_vline(xintercept = mu, col='darkred')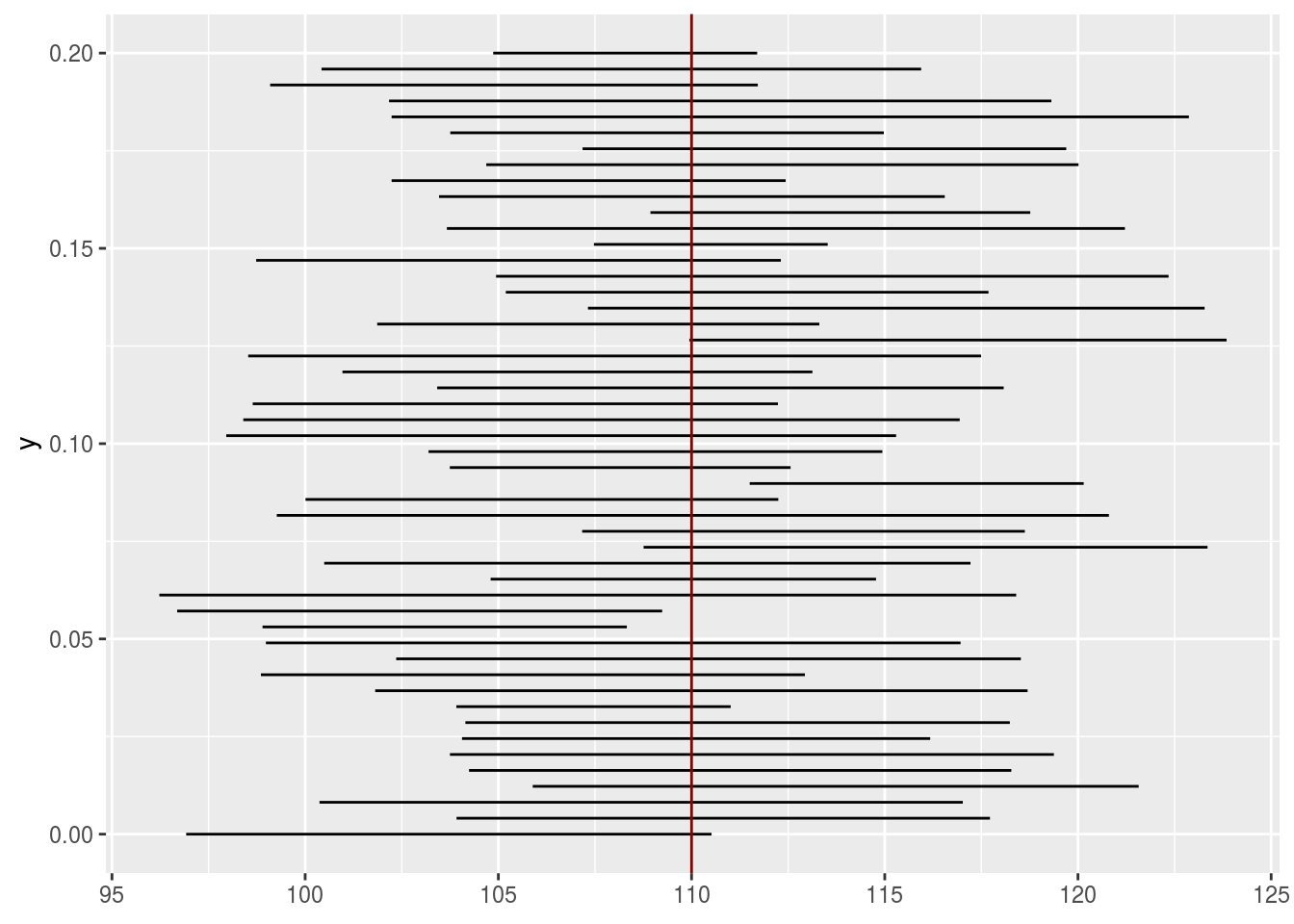
La statistique inférentielle - résumé
Ce qu’on vient de voir sur l’exemple de la moyenne de la population est l’exemple de base de la statistique inférentielle. Plus généralement, on s’intéresse à une quantité spécifique d’une population donnée. On n’a jamais accès à cette quantitté mais on peut en avoir une idée grâce à une sous partie de la population, un échantillon.
A partir de cette échantillon, on peut construire une quantité qui va approcher la quantité d’intéêt dans la population. La façon de construire cette quantité repose sur la théorie de l’estimation que l’on verra dans le chapitre Estimation par maximum de vraisemblance.
Loi d’un estimateur
Un estimateur est une variable aléatoire. La loi de cette variable aléatoire repose sur des hyypothèses portant sur l’échantillonnage et sur la distribution de la quantité d’intérêt dans la population. Elle permet de construire des intervalles de confiance et des tests.
Une réalisation de l’estimateur est une estimation. C’est la valeur que prend l’estimateur dans l’échantillon observé.
Intervalles de confiance
A partir des estimation et des hypothèses de distribution on peut construire un intervalle de confiance pour la quantité d’intérêt. C’set un intervalle pour lequel on peut affirmer qu’il contient la valeur de la quantité d’intérêt avec un risque de se tromper contrôlé.
Les tests statistiques
Grâce à la loi de l’estimteur on peut construire des tests statistiques qui vont permettre de tester des hypothèses sur la quantité d’intérêt. Est ce que la quantité d’intérêt est inférieur ou égale à une certaine valeur par exemple.
La mise en oeuvre du test permet de réfuter (ou non) l’hypothèse, avec un risque de réfuter à tort qui est controlé.