Rappels de statistique élémentaire
Modèles linéaires
Modèle de régression simple
Le fichier data/T_Oir_StHilaire_87_02.txt contient des relevés journaliers de la température de l’eau et de la température de l’air dans l’Oir, un petit fleuve côtier de Basse Normandie. Données journalières. On se pose la question du lien entre la température de l’eau et la température de l’air.
Visualisation des données de température
Une première étape essentielle consiste à visualiser les données. Proposer un code permettant de produire le graphique ci dessous~:
Transformation de la date en jours calendaires’une chaîne de caractères en dates.
df_temp <- df_temp %>% mutate(date_posixct = as.POSIXct(strptime(df_temp$date, format = "%d/%m/%Y"))) 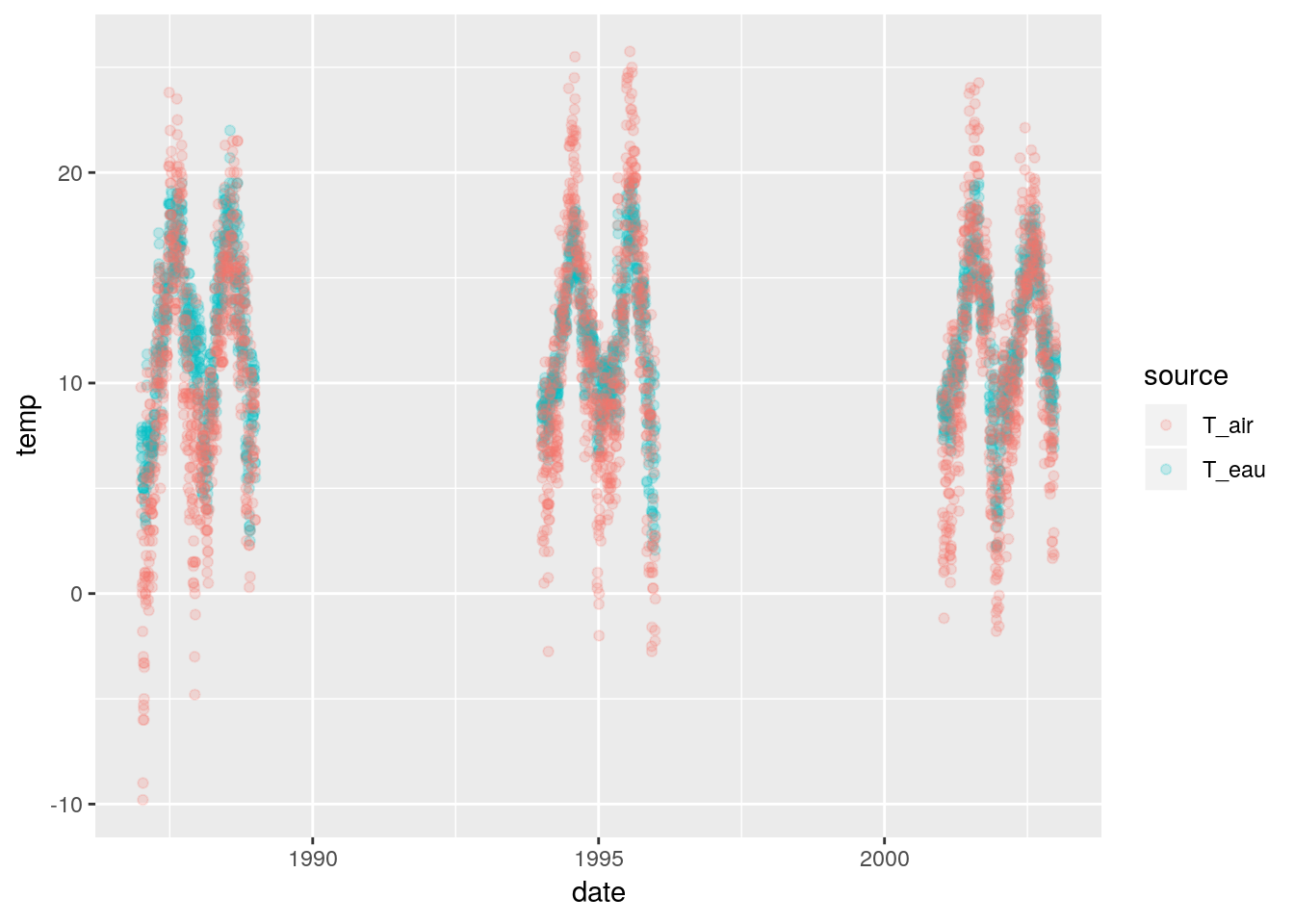
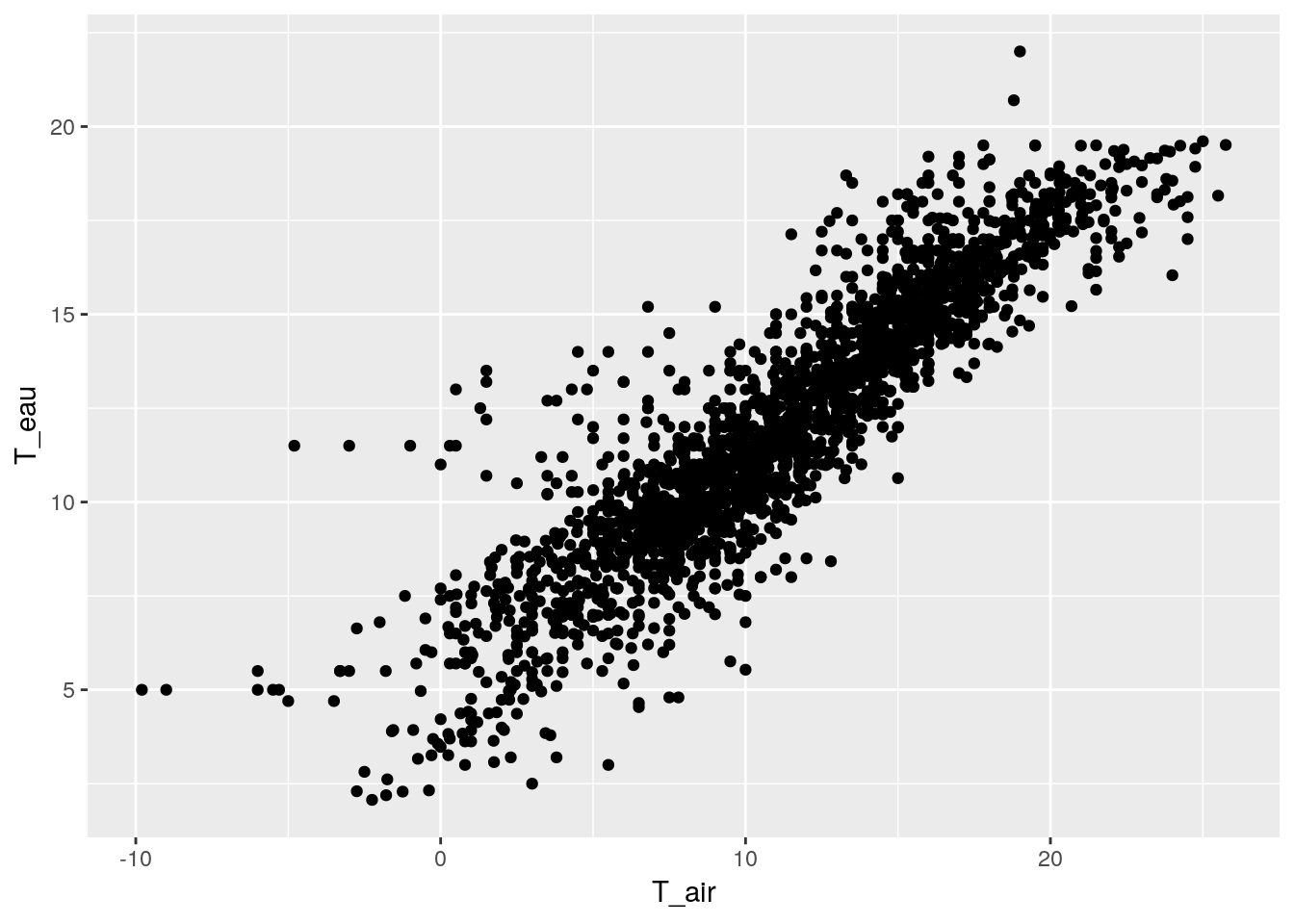
Le modèle de régression simple
Le modèle de la régression simple s’écrit mathématiquement sous la forme suivante :
\[ Y_k = \alpha + \beta x_k + E_k, \quad E_k \overset{i.i.d}{\sim}\mathcal{N}(0, \sigma^2),\] où
- \(Y_k\) désigne la température de l’eau de la k$^{} mesure,
- \(x_k\) désigne la température de l’air de la k$^{} mesure,
- \(E_k\) est un terme d’écart au modèle pour la mesure \(k\), on suppose qu’il suit une loi normale centrée de variance inconnue \(\sigma^2\),
- \(\alpha\) est le paramètre inconnu qui ajuste l’ordonnée à l’origine,
- \(\beta\) est le paramètre inconnu qui règle le lien entre température de l’air et température de l’eau.
Estimation des paramètres
L’estimation consiste à déterminer le choix des paramètre \(\alpha\) et \(\beta\) les plus pertinents. Une méthode générique d’estimation des paramètres d’un modèle statistique, consiste à optimiser une fonction nommée la vraisemblance, on le verra plus tard.
Dans un premier temps, on cherche à trouver la droite d’équation \(y=a +bx\) qui résume au mieux les données, i.e on cherche à minimiser l’écart entre nos observations \(y_i\) et la prédiction par le modèle \(\alpha + \beta x_i\), ce qui revient à trouver le minimum de la fonction
\[MCO(\alpha, \beta; \boldsymbol{y},\boldsymbol{x}) = \sum_{i=1}^{n} \{y_i - (\alpha + \beta x_i) \}^2. \]
La commande lm de R fait le travail, dans la commande suivante :
lm_eau_air <- lm(T_eau ~ T_air, data=df_temp)Avant toute analyse, il est indispensable de discuter les hypothèses du modèle. Il est pour cela utile de regarder les graphiques de diagnostic
autoplot(lm_eau_air, data=df_temp)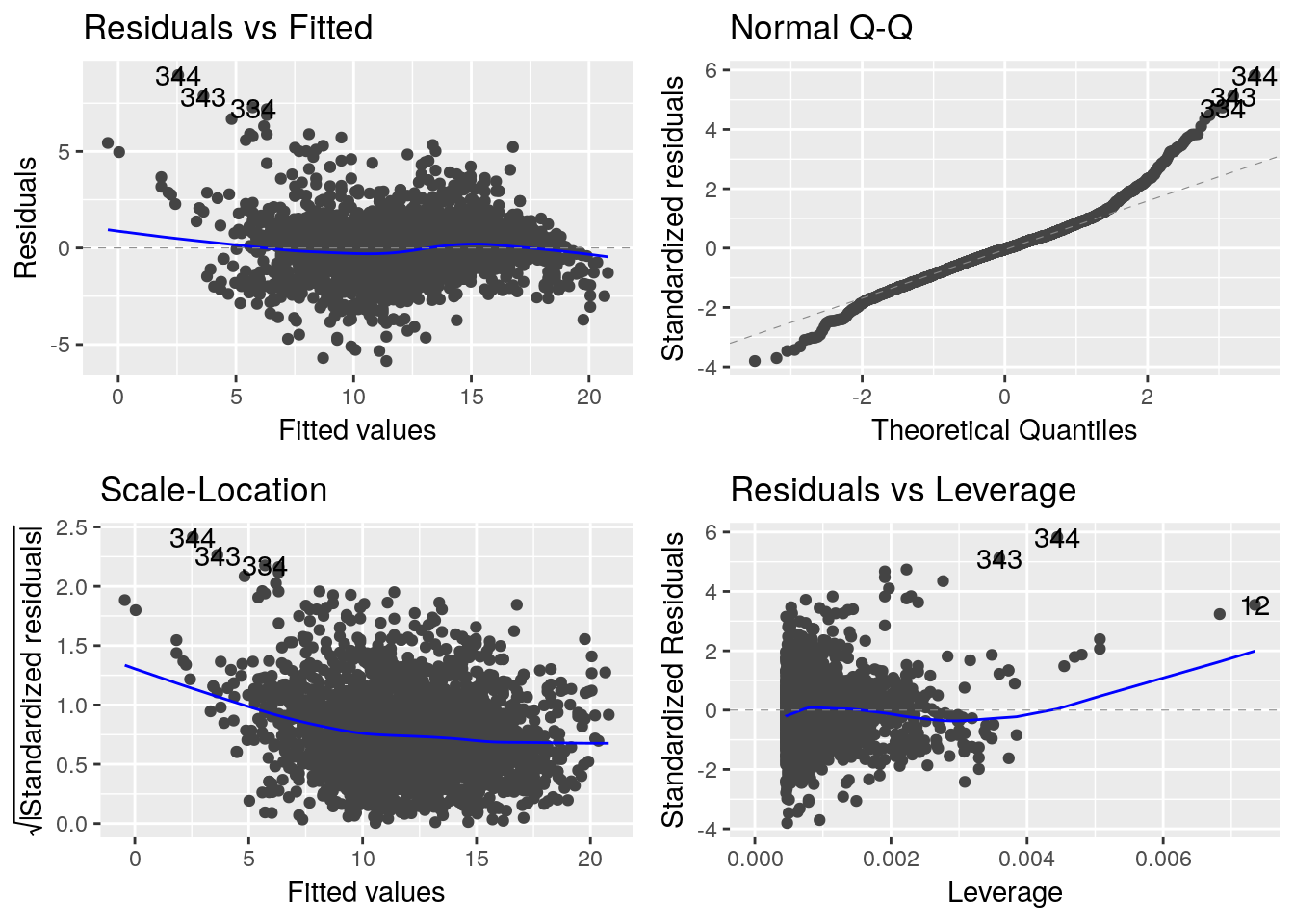
On peut obtenir les coefficients estimés du modèle grâce à la commande :
coef(lm_eau_air)## (Intercept) T_air
## 5.4149067 0.5976255On a non seulement ces valeurs mais les tests de nullité des paramètre associés grâce à la commande :
summary(lm_eau_air)##
## Call:
## lm(formula = T_eau ~ T_air, data = df_temp)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.8562 -0.9267 -0.0471 0.7730 8.9537
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.414907 0.075402 71.81 <2e-16 ***
## T_air 0.597626 0.006115 97.72 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.539 on 2189 degrees of freedom
## Multiple R-squared: 0.8135, Adjusted R-squared: 0.8134
## F-statistic: 9550 on 1 and 2189 DF, p-value: < 2.2e-16Le test nous indique l’existence d’un lien entre la température de l’eau et la température de l’air. On peut utiliser ce modèle pour prédire la température de l’eau à partir de la température de l’air. Il faut faire attention à ce que l’on veut prédire.
df_pred <- as.tibble(predict(lm_eau_air, interval="confidence")) %>% dplyr::select(fit =fit, lwr_conf = lwr, upr_conf = upr) %>% bind_cols(as.tibble(predict(lm_eau_air, interval="prediction"))) %>% select(-fit1, lwr_predict =lwr, upr_predict = upr) %>% bind_cols(df_temp)## Warning in predict.lm(lm_eau_air, interval = "prediction"): predictions on current data refer to _future_ responsesggplot(data = df_pred, aes(x = T_air, y = T_eau)) +
geom_point(alpha=0.2) +
geom_smooth(method = 'lm', se = TRUE) +
geom_line(data=df_pred, aes(y=lwr_conf), col='red', linetype='dotted') +
geom_line(data=df_pred, aes(y=upr_conf), col='red', linetype='dotted') +
geom_line(data=df_pred, aes(y=lwr_predict), col='green', linetype='dashed') +
geom_line(data=df_pred, aes(y=upr_predict), col='green', linetype='dashed') 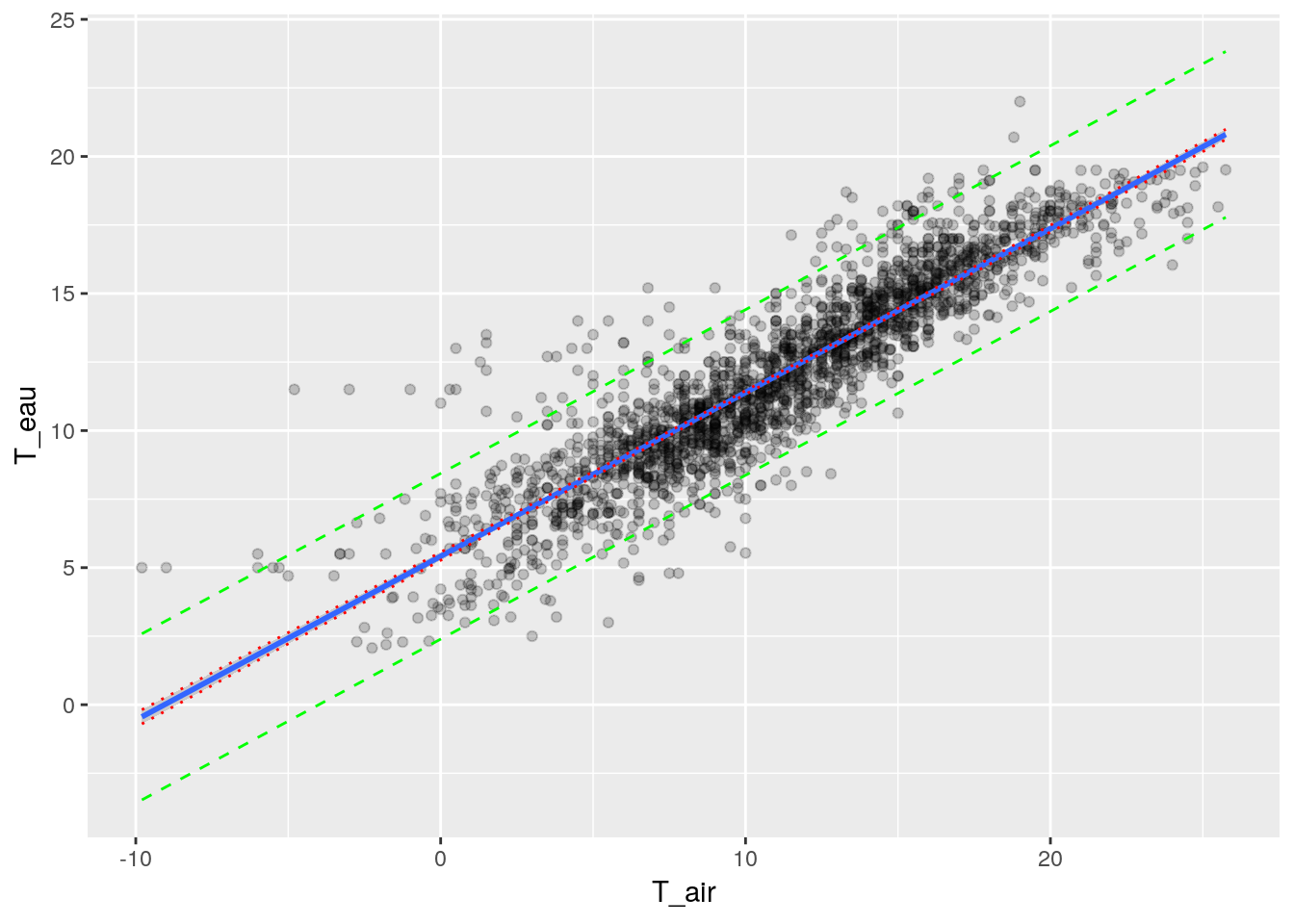
La question se pose également de savoir si la température moyenne annuelle de l’eau change d’une année sur l’autre, c’est à dire peut on mettre en évidence une tendance climatique. Pour cela, on chercher à explorer un lien entre la température de l’eau et l’année. On cherche donc à explorer le lien entre une variable quantitative (la température) et une variable qualitative (l’année). C’est un modèle d’analyse de la variance.
Analyse de la variance
Analyse de la variance à 1 facteur
ggplot(data=df_temp, aes(x = as.factor(annee), y = T_eau)) + geom_boxplot()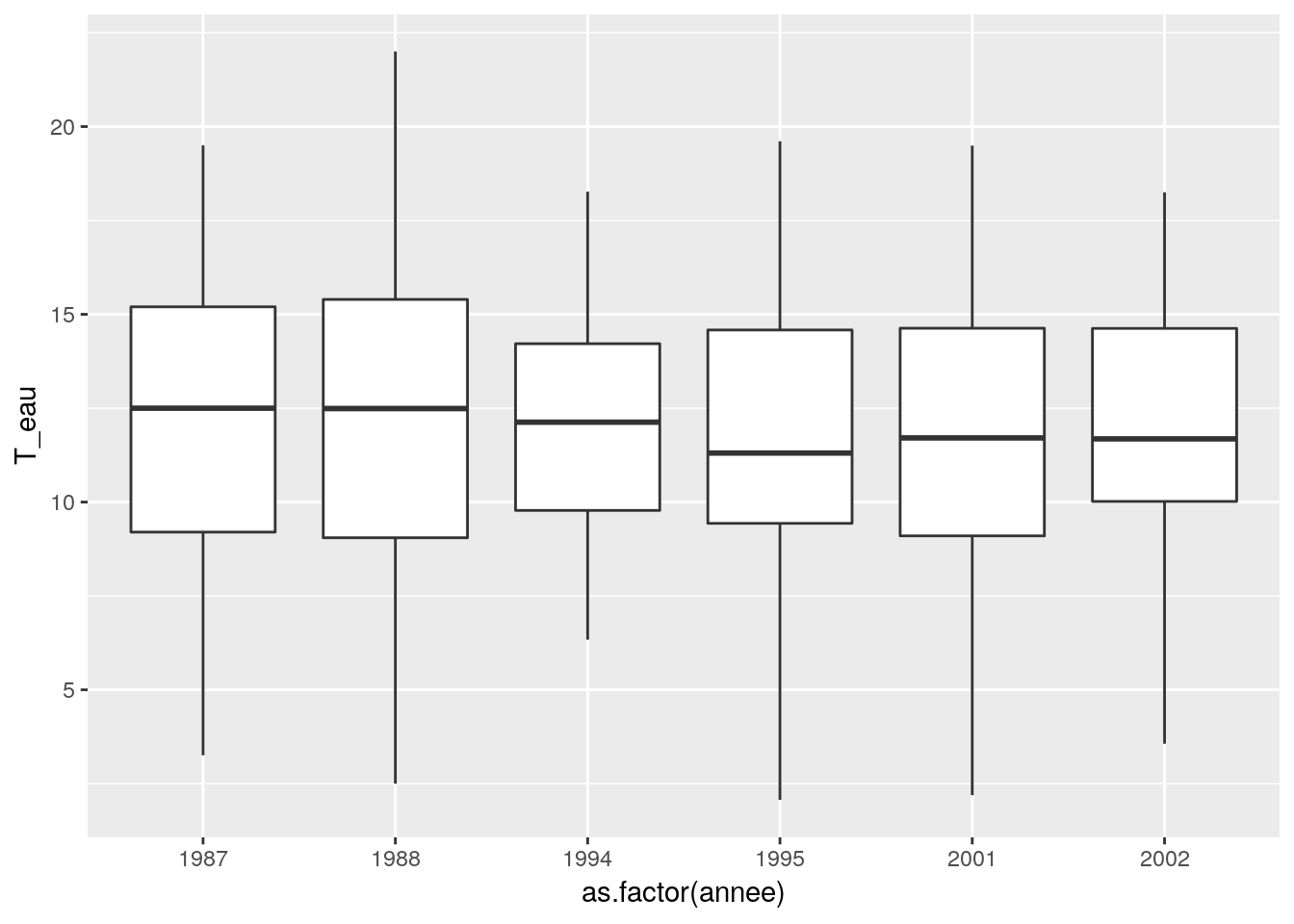
Il ne semble pas y avoir d’effet année, on peut néanmoins le vérifier.
Le modèle s’écrit sous la forme suivante:
\[ Y_{ik} = \mu + \alpha_i + E_{ik}, \quad E_{ik} \overset{i.i.d}{\sim}\mathcal{N}(0, \sigma^2),\]
où
- \(Y_{ik}\) désigne la température de l’eau de la k\(^{\mbox{ème}}\) mesure de l’année \(i\),
- \(E_{ik}\) est un terme d’écart au modèle pour la mesure \(k\) de l’année \(i\),
- \(\mu\) est le paramètre inconnu qui ajuste l’ordonnée à l’origine commune à toutes les années,
- \(\alpha_i\) est le paramètre inconnu qui ajuste la différence entre l’ordonnée à l’origine commune à toutes les années et celle de l’année \(i\).
lm1 <- lm(T_eau ~ annee, data = df_temp)
summary(lm1)##
## Call:
## lm(formula = T_eau ~ annee, data = df_temp)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.9724 -2.5404 -0.1151 2.7758 9.8849
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 33.32906 26.46860 1.259 0.208
## annee -0.01067 0.01327 -0.804 0.421
##
## Residual standard error: 3.564 on 2189 degrees of freedom
## Multiple R-squared: 0.0002953, Adjusted R-squared: -0.0001614
## F-statistic: 0.6466 on 1 and 2189 DF, p-value: 0.4214On constate qu’un seul paramètre est estimé pour l’année or nous en attendions un par année. C’est le comportement objet de R qui lui indique de faire une régression linéaire et non une analyse de la variance. La variable année est en effet de classe numeric. Il faut indique que l’année doit être traitée comme une variable qualitative, pour faire la différence on peut créer une nouvelle variable annee_fact
df_temp$annee_fact <- as.factor(df_temp$annee)
lm_eau_annee <- lm(T_eau~annee_fact, data = df_temp)
summary(lm_eau_annee)##
## Call:
## lm(formula = T_eau ~ annee_fact, data = df_temp)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.8304 -2.5093 -0.1222 2.7800 9.8319
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 12.12217 0.18663 64.951 <2e-16 ***
## annee_fact1988 0.04589 0.26376 0.174 0.862
## annee_fact1994 -0.01615 0.26394 -0.061 0.951
## annee_fact1995 -0.22373 0.26394 -0.848 0.397
## annee_fact2001 -0.28115 0.26394 -1.065 0.287
## annee_fact2002 0.01639 0.26394 0.062 0.950
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.566 on 2185 degrees of freedom
## Multiple R-squared: 0.001269, Adjusted R-squared: -0.001016
## F-statistic: 0.5552 on 5 and 2185 DF, p-value: 0.7344lm_0 <- lm(T_eau~1, data = df_temp)
anova(lm_0, lm_eau_annee)## Analysis of Variance Table
##
## Model 1: T_eau ~ 1
## Model 2: T_eau ~ annee_fact
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 2190 27815
## 2 2185 27780 5 35.296 0.5552 0.7344Discutons ici de la contrainte d’identifiabilité sur les \(\alpha\).
Avant toute chose, vérifions la validité des hypothèses sur les résidus.
autoplot(lm_eau_annee, data = df_temp)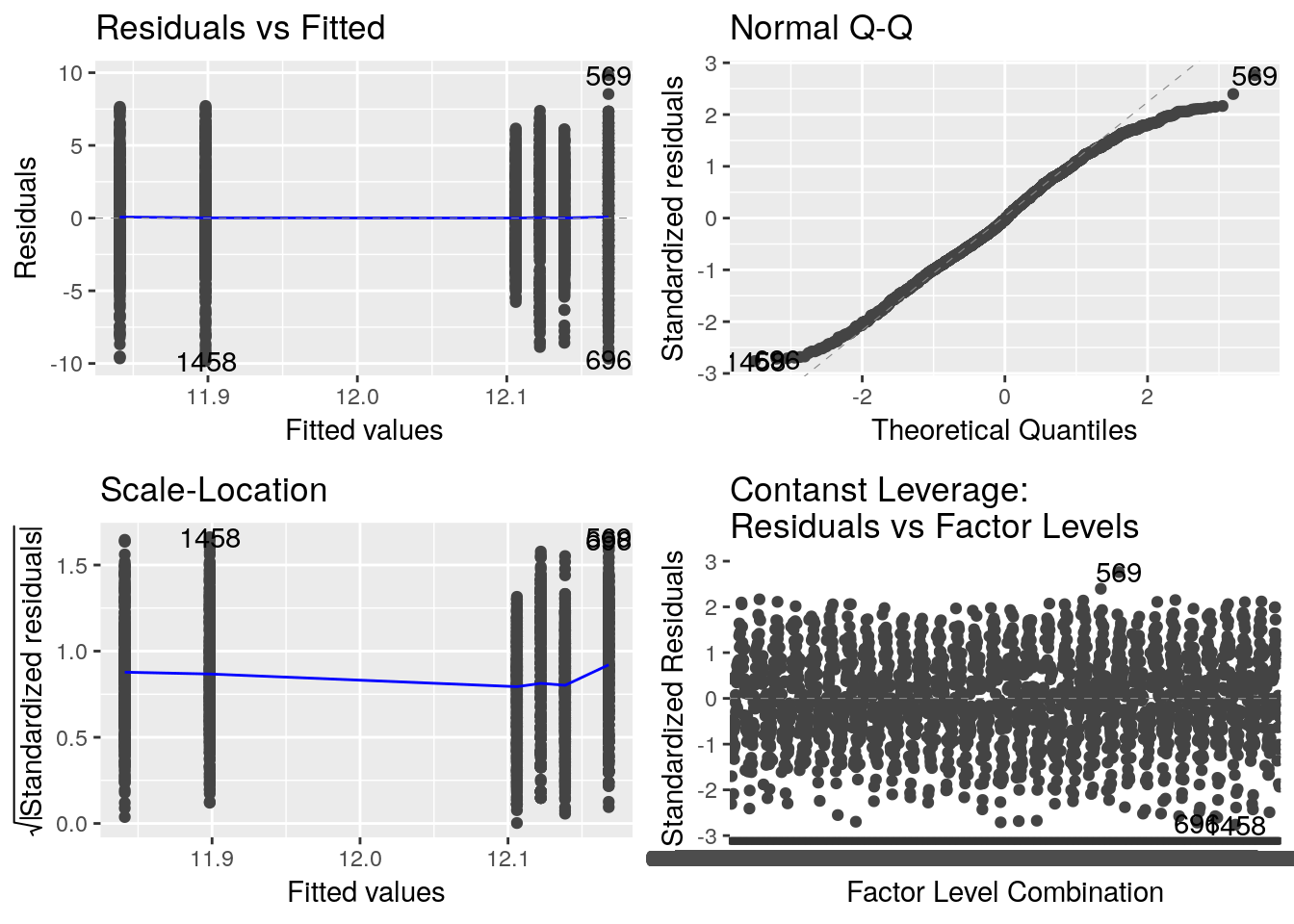
On peut tester l’effet année:
anova(lm_eau_annee)## Analysis of Variance Table
##
## Response: T_eau
## Df Sum Sq Mean Sq F value Pr(>F)
## annee_fact 5 35.3 7.0592 0.5552 0.7344
## Residuals 2185 27779.8 12.7138Sans grande surprise, on ne met pas en évidence d’effet années, mais on constate également que la variance est très grande.
Néanmoins il est possible que cette absence d’effet année soit du à une trop grande variabilité du fait de la variabilité annuelle de la température au cours de l’année.
Analyse de la variance à 2 facteurs
ggplot(data = df_temp, aes(x = as.factor(mois), y = T_eau)) + geom_boxplot()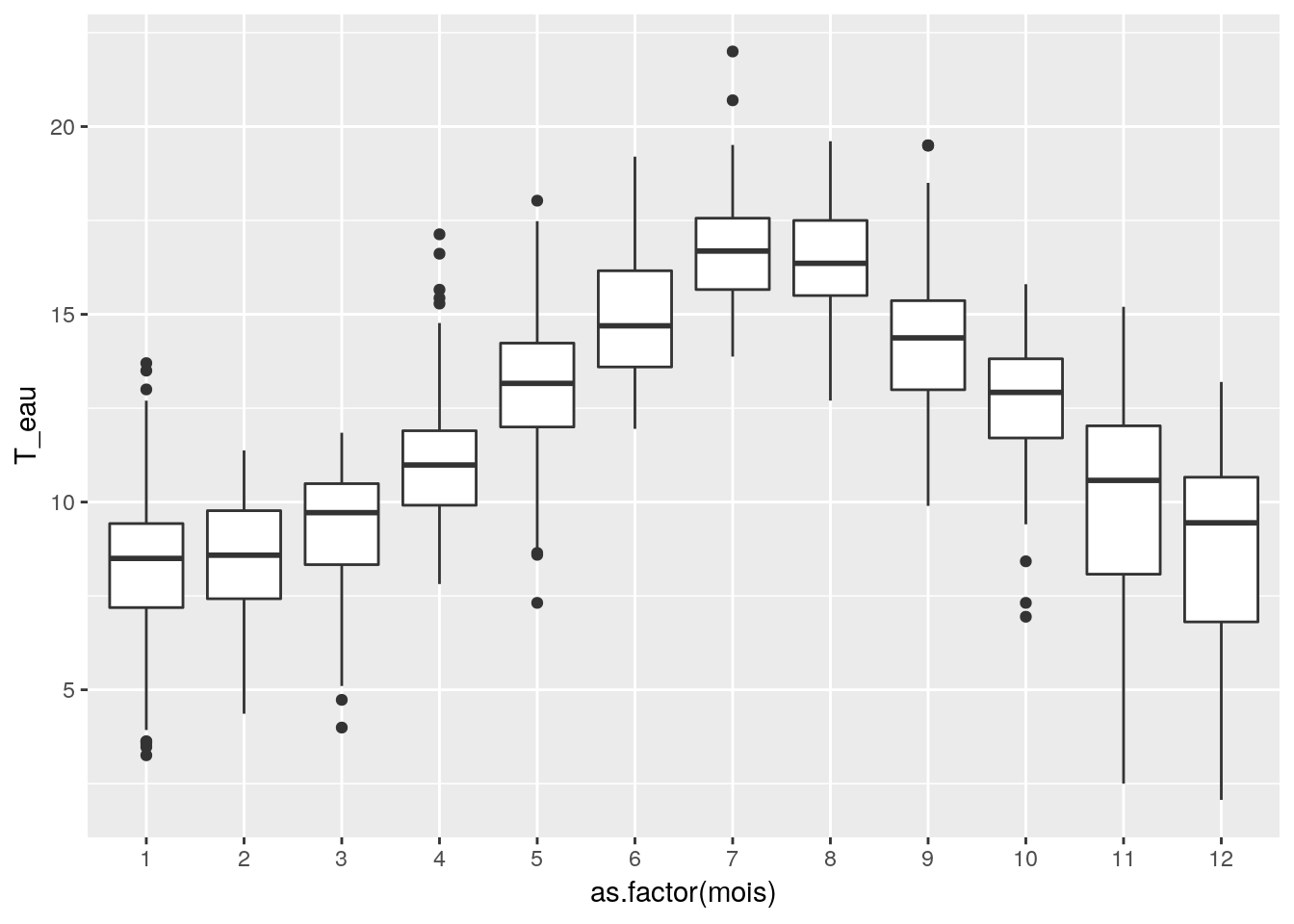
ggplot(data = df_temp, aes(x = as.factor(mois), y = T_eau, col=annee_fact)) + geom_boxplot()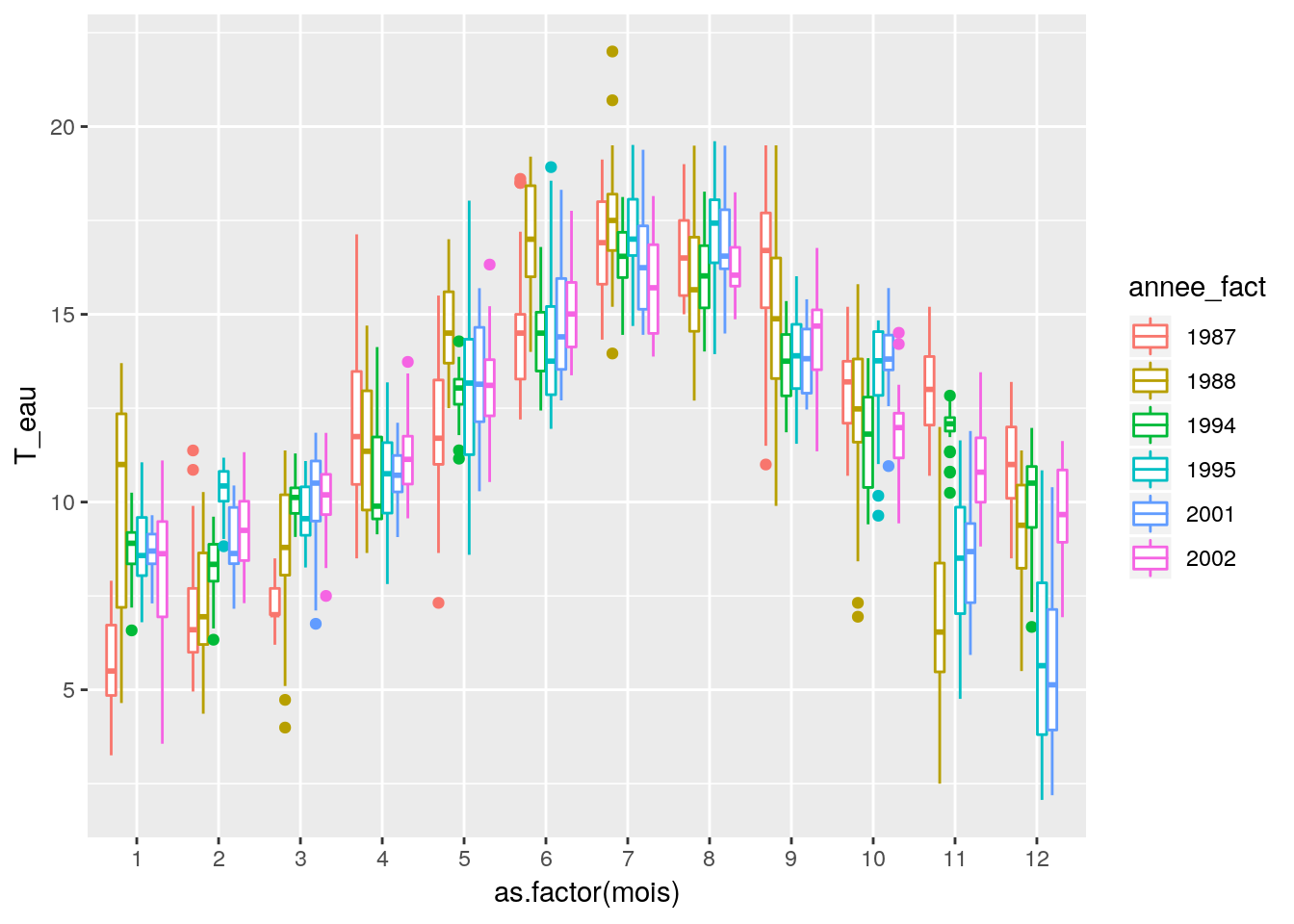
On veut donc expliquer la température en fonction de l’année et du mois. Le modèle s’écrit sous la forme suivante:
\[ Y_{ijk} = \mu + \alpha_i +\beta_j +\gamma_{ij} + E_{ijk}, \quad E_{ijk} \overset{i.i.d}{\sim}\mathcal{N}(0, \sigma^2),\]
où
- \(Y_{ik}\) désigne la température de l’eau de la k\(^{\mbox{ème}}\) mesure de l’année \(i\),
- \(E_{ik}\) est un terme d’écart au modèle pour la mesure \(k\) de l’année \(i\),
- \(\mu\) est le paramètre inconnu qui ajuste l’ordonnée à l’origine commune à toutes les années,
- \(\alpha_i\) est le paramètre inconnu qui ajuste la différence entre l’ordonnée à l’origine commune à toutes les années et celle de l’année \(i\),
- \(\beta_j\) est le paramètre inconnu qui ajuste la différence entre l’ordonnée à l’origine commune à toutes les années et celle du mois \(j\),
- \(\gamma_{ij}\) est le paramètre inconnu qui quantifie l’interaction entre l’année \(i\) et le mois \(j\).
Il est important de regarder le plan d’expérience pour détecter des potentiels déséquilibres dans le dispositif expérimental.
with(df_temp, table(mois, annee_fact))## annee_fact
## mois 1987 1988 1994 1995 2001 2002
## 1 31 31 31 31 31 31
## 2 28 29 28 28 28 28
## 3 31 31 31 31 31 31
## 4 30 30 30 30 30 30
## 5 31 31 31 31 31 31
## 6 30 30 30 30 30 30
## 7 31 31 31 31 31 31
## 8 31 31 31 31 31 31
## 9 30 30 30 30 30 30
## 10 31 31 31 31 31 31
## 11 30 30 30 30 30 30
## 12 31 31 31 31 31 31Le plan d’expérience est quasimment équilibré.
On peut par ailleurs suspecterl’effet d’une interaction entre les facteurs, on peut visualiser cette potentielle interaction en regardant le graphique d’interaction.
df_temp$mois_fact <- as.factor(df_temp$mois)
with( df_temp,
interaction.plot(trace.factor = annee_fact, x.factor = mois, response = T_eau) )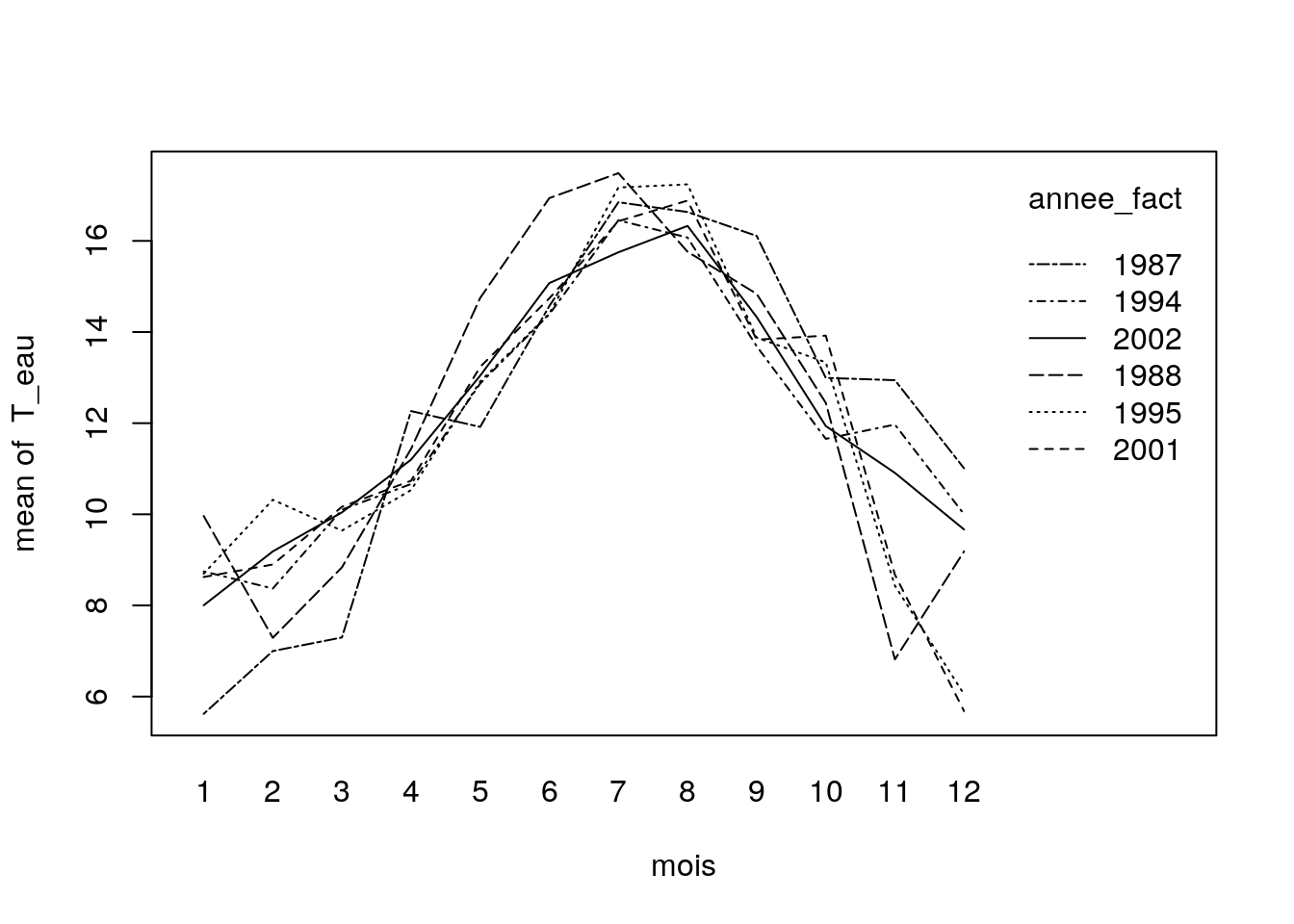
Ou en plus joli
df_temp %>%
ggplot() +
aes(x = mois_fact, color = annee_fact, group = annee_fact, y = T_eau) +
stat_summary(fun.y = mean, geom = "point") +
stat_summary(fun.y = mean, geom = "line")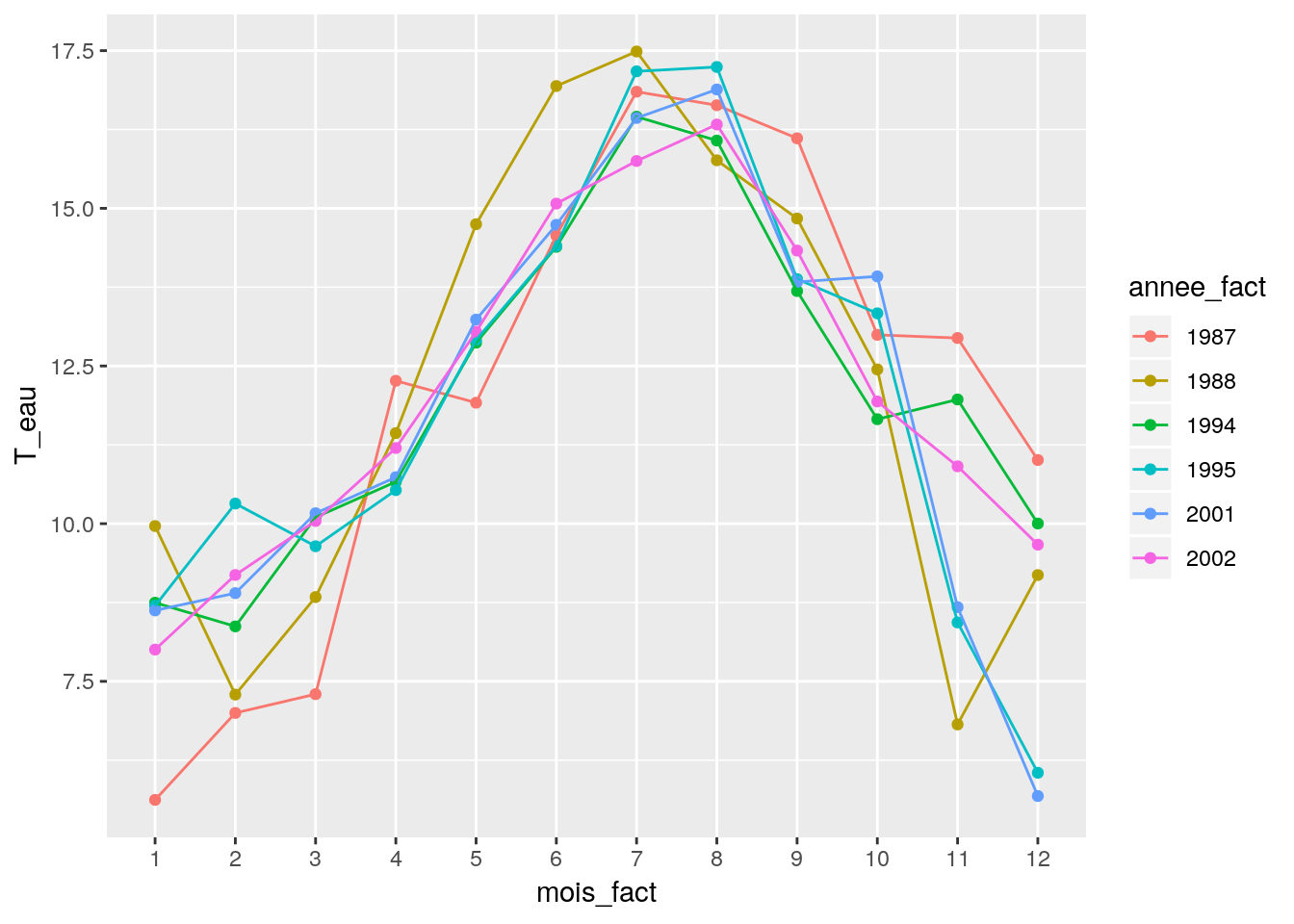
Ce graphique semble indiquer l’existence d’interactions entre les deux facteurs.
On peut maintenant auster un modèle d’anlyse de la variance à 2 facteurs.
lm_eau_annee_mois <- lm(T_eau ~ annee_fact + mois_fact + annee_fact:mois_fact, data = df_temp)
autoplot(lm_eau_annee_mois, data = df_temp)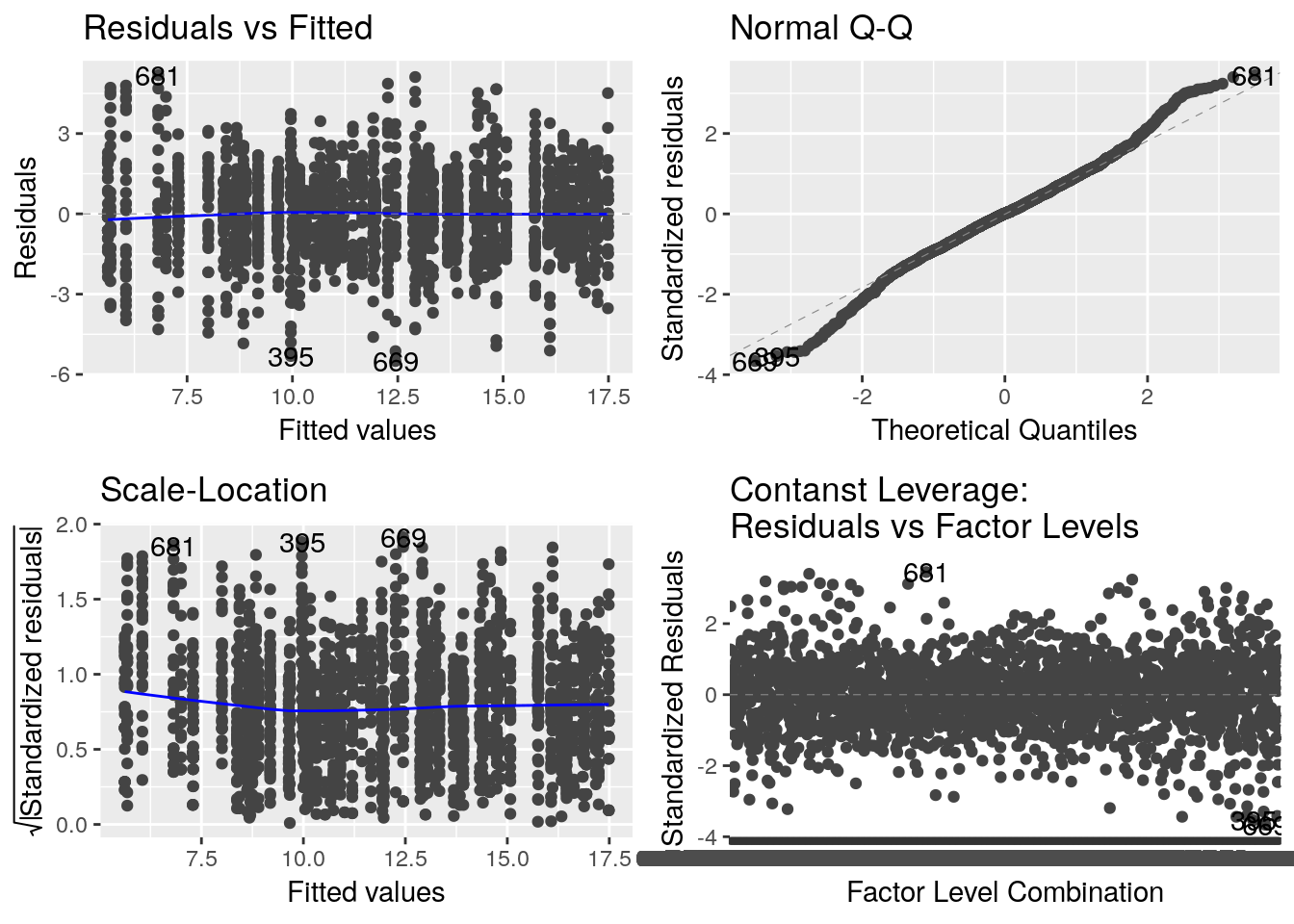
Les tests des différents effets sont testés dans la table d’anlayse de la variance suivante
anova(lm_eau_annee_mois)## Analysis of Variance Table
##
## Response: T_eau
## Df Sum Sq Mean Sq F value Pr(>F)
## annee_fact 5 35.3 7.06 3.0262 0.009993 **
## mois_fact 11 19871.0 1806.45 774.4020 < 2.2e-16 ***
## annee_fact:mois_fact 55 2965.8 53.92 23.1162 < 2.2e-16 ***
## Residuals 2119 4943.0 2.33
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Anova(lm_eau_annee_mois)## Anova Table (Type II tests)
##
## Response: T_eau
## Sum Sq Df F value Pr(>F)
## annee_fact 36.2 5 3.103 0.008535 **
## mois_fact 19871.0 11 774.402 < 2.2e-16 ***
## annee_fact:mois_fact 2965.8 55 23.116 < 2.2e-16 ***
## Residuals 4943.0 2119
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Les estimations des différents paramètres sont données dans la table
summary(lm_eau_annee_mois)##
## Call:
## lm(formula = T_eau ~ annee_fact + mois_fact + annee_fact:mois_fact,
## data = df_temp)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.4996 -0.9342 0.0132 0.9145 5.1837
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.6203 0.2743 20.488 < 2e-16 ***
## annee_fact1988 4.3423 0.3879 11.193 < 2e-16 ***
## annee_fact1994 3.1264 0.3879 8.059 1.27e-15 ***
## annee_fact1995 3.0773 0.3879 7.932 3.45e-15 ***
## annee_fact2001 3.0036 0.3879 7.743 1.50e-14 ***
## annee_fact2002 2.3832 0.3879 6.143 9.64e-10 ***
## mois_fact2 1.3787 0.3982 3.462 0.000546 ***
## mois_fact3 1.6765 0.3879 4.322 1.62e-05 ***
## mois_fact4 6.6453 0.3912 16.989 < 2e-16 ***
## mois_fact5 6.2974 0.3879 16.233 < 2e-16 ***
## mois_fact6 8.9500 0.3912 22.881 < 2e-16 ***
## mois_fact7 11.2285 0.3879 28.944 < 2e-16 ***
## mois_fact8 11.0140 0.3879 28.391 < 2e-16 ***
## mois_fact9 10.4897 0.3912 26.817 < 2e-16 ***
## mois_fact10 7.3733 0.3879 19.006 < 2e-16 ***
## mois_fact11 7.3231 0.3912 18.721 < 2e-16 ***
## mois_fact12 5.3894 0.3879 13.892 < 2e-16 ***
## annee_fact1988:mois_fact2 -4.0516 0.5606 -7.228 6.83e-13 ***
## annee_fact1994:mois_fact2 -1.7543 0.5631 -3.115 0.001862 **
## annee_fact1995:mois_fact2 0.2425 0.5631 0.431 0.666739
## annee_fact2001:mois_fact2 -1.1041 0.5631 -1.961 0.050050 .
## annee_fact2002:mois_fact2 -0.1957 0.5631 -0.348 0.728192
## annee_fact1988:mois_fact3 -2.8026 0.5486 -5.108 3.54e-07 ***
## annee_fact1994:mois_fact3 -0.3220 0.5486 -0.587 0.557361
## annee_fact1995:mois_fact3 -0.7324 0.5486 -1.335 0.182039
## annee_fact2001:mois_fact3 -0.1352 0.5486 -0.246 0.805426
## annee_fact2002:mois_fact3 0.3628 0.5486 0.661 0.508457
## annee_fact1988:mois_fact4 -5.1722 0.5532 -9.350 < 2e-16 ***
## annee_fact1994:mois_fact4 -4.7281 0.5532 -8.547 < 2e-16 ***
## annee_fact1995:mois_fact4 -4.8114 0.5532 -8.698 < 2e-16 ***
## annee_fact2001:mois_fact4 -4.5324 0.5532 -8.193 4.34e-16 ***
## annee_fact2002:mois_fact4 -3.4490 0.5532 -6.235 5.44e-10 ***
## annee_fact1988:mois_fact5 -1.5115 0.5486 -2.755 0.005918 **
## annee_fact1994:mois_fact5 -2.1747 0.5486 -3.964 7.62e-05 ***
## annee_fact1995:mois_fact5 -2.0810 0.5486 -3.793 0.000153 ***
## annee_fact2001:mois_fact5 -1.6853 0.5486 -3.072 0.002155 **
## annee_fact2002:mois_fact5 -1.2585 0.5486 -2.294 0.021889 *
## annee_fact1988:mois_fact6 -1.9736 0.5532 -3.568 0.000368 ***
## annee_fact1994:mois_fact6 -3.3070 0.5532 -5.978 2.64e-09 ***
## annee_fact1995:mois_fact6 -3.2450 0.5532 -5.866 5.17e-09 ***
## annee_fact2001:mois_fact6 -2.8349 0.5532 -5.125 3.25e-07 ***
## annee_fact2002:mois_fact6 -1.8789 0.5532 -3.397 0.000695 ***
## annee_fact1988:mois_fact7 -3.7042 0.5486 -6.752 1.88e-11 ***
## annee_fact1994:mois_fact7 -3.5223 0.5486 -6.420 1.68e-10 ***
## annee_fact1995:mois_fact7 -2.7542 0.5486 -5.020 5.59e-07 ***
## annee_fact2001:mois_fact7 -3.4201 0.5486 -6.234 5.48e-10 ***
## annee_fact2002:mois_fact7 -3.4814 0.5486 -6.346 2.70e-10 ***
## annee_fact1988:mois_fact8 -5.2149 0.5486 -9.505 < 2e-16 ***
## annee_fact1994:mois_fact8 -3.6863 0.5486 -6.719 2.34e-11 ***
## annee_fact1995:mois_fact8 -2.4703 0.5486 -4.503 7.08e-06 ***
## annee_fact2001:mois_fact8 -2.7532 0.5486 -5.018 5.65e-07 ***
## annee_fact2002:mois_fact8 -2.6881 0.5486 -4.900 1.03e-06 ***
## annee_fact1988:mois_fact9 -5.6136 0.5532 -10.148 < 2e-16 ***
## annee_fact1994:mois_fact9 -5.5482 0.5532 -10.030 < 2e-16 ***
## annee_fact1995:mois_fact9 -5.3089 0.5532 -9.597 < 2e-16 ***
## annee_fact2001:mois_fact9 -5.2808 0.5532 -9.546 < 2e-16 ***
## annee_fact2002:mois_fact9 -4.1629 0.5532 -7.525 7.73e-14 ***
## annee_fact1988:mois_fact10 -4.8903 0.5486 -8.914 < 2e-16 ***
## annee_fact1994:mois_fact10 -4.4639 0.5486 -8.136 6.86e-16 ***
## annee_fact1995:mois_fact10 -2.7359 0.5486 -4.987 6.64e-07 ***
## annee_fact2001:mois_fact10 -2.0763 0.5486 -3.785 0.000158 ***
## annee_fact2002:mois_fact10 -3.4396 0.5486 -6.269 4.38e-10 ***
## annee_fact1988:mois_fact11 -10.4693 0.5532 -18.926 < 2e-16 ***
## annee_fact1994:mois_fact11 -4.1008 0.5532 -7.413 1.77e-13 ***
## annee_fact1995:mois_fact11 -7.5866 0.5532 -13.714 < 2e-16 ***
## annee_fact2001:mois_fact11 -7.2710 0.5532 -13.144 < 2e-16 ***
## annee_fact2002:mois_fact11 -4.4173 0.5532 -7.985 2.28e-15 ***
## annee_fact1988:mois_fact12 -6.1670 0.5486 -11.241 < 2e-16 ***
## annee_fact1994:mois_fact12 -4.1336 0.5486 -7.534 7.22e-14 ***
## annee_fact1995:mois_fact12 -8.0365 0.5486 -14.648 < 2e-16 ***
## annee_fact2001:mois_fact12 -8.3319 0.5486 -15.187 < 2e-16 ***
## annee_fact2002:mois_fact12 -3.7257 0.5486 -6.791 1.44e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.527 on 2119 degrees of freedom
## Multiple R-squared: 0.8223, Adjusted R-squared: 0.8163
## F-statistic: 138.1 on 71 and 2119 DF, p-value: < 2.2e-16On a constaté un lien entre température de l’air et température l’eau et un effet de l’année et une effet du mois.
Supposons que la température de l’air contient déjà le signal des variations saisonnières. (il faudrait le vérifier).
On peut se demander si le lien liant température de l’air et température de l’eau est le même quelle que soit l’année. Ce qui nous amène à examiner le lien entre une variable quantitative (la température de l’eau) et deux variables dont l’une est quantitative (tempéraiture de l’autre ) et l’autre qualitative. C’est le modèle d’analyse de la covariance.
Analyse de la covariance
Pour tester cette hypothèse, on écrit un modèle dans lequel on autorise une relation différente chaque année :
\[ Y_{ik} = \mu + \alpha_i + \beta x_{ik} + \gamma x_{ik} + E_{ik}, \quad E_{ik} \overset{i.i.d}{\sim}\mathcal{N}(0, \sigma^2),\]
où
\(Y_{ik}\) désigne la température de l’eau de la k\(^{\mbox{ème}}\) mesure de l’année \(i\),
- \(x_k\) désigne la température de l’air de la k\(^{\mbox{ème}}\) mesure de l’année \(i\),
- \(E_k\) est un terme d’écart au modèle pour la mesure \(k\) de l’année \(i\),
- \(\mu\) est le paramètre inconnu qui ajuste l’ordonnée à l’origine commune à toutes les années,
- \(\alpha_i\) est le paramètre inconnu qui ajuste la différence entre l’ordonnée à l’origine commune à toutes les années et celle de l’année \(i\) ,
- \(\beta\) est le paramètre inconnu qui règle le lien, commun à toutes les années, entre température de l’air et température de l’eau,
\(\gamma_i\) est le paramètre inconnu qui règle la différence entre la pente commune à toutes les années et la pente de l’année \(i\).
df_temp$annee_fact <- as.factor(df_temp$annee)
ggplot(data=df_temp, aes(x = T_air, y = T_eau, col = annee_fact)) + geom_point(alpha=0.1) + guides(col=guide_legend(title = "Année")) +
geom_smooth(method = "lm", se = FALSE)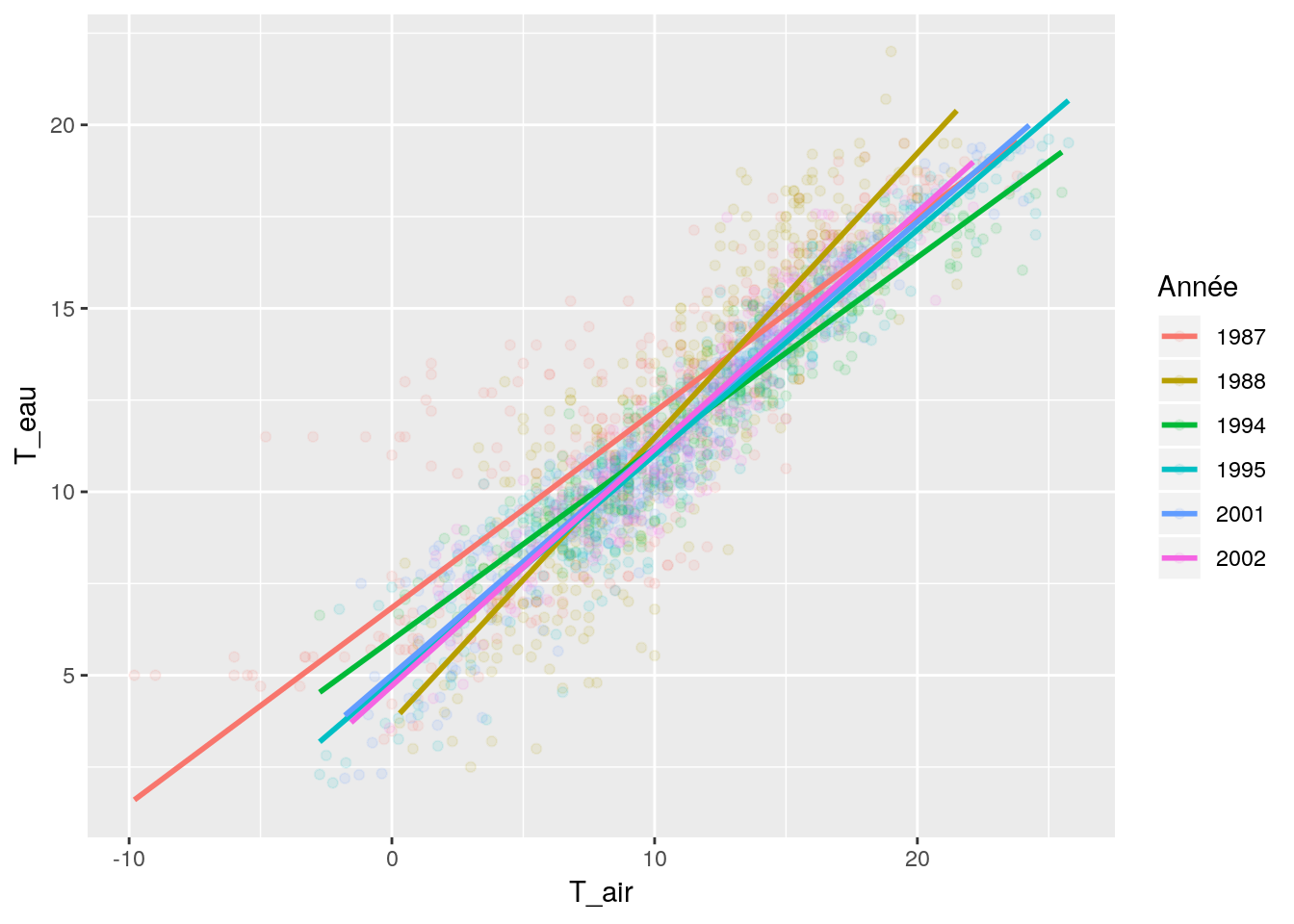
lm_eau_air_annee <- lm( T_eau ~ annee + T_air + annee: T_air, data = df_temp)
summary(lm_eau_air_annee)##
## Call:
## lm(formula = T_eau ~ annee + T_air + annee:T_air, data = df_temp)
##
## Residuals:
## Min 1Q Median 3Q Max
## -6.1868 -0.9101 0.0457 0.8298 8.4296
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 148.263258 25.561853 5.800 7.59e-09 ***
## annee -0.071651 0.012821 -5.588 2.58e-08 ***
## T_air -3.243721 2.114907 -1.534 0.1252
## annee:T_air 0.001928 0.001061 1.818 0.0692 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.511 on 2187 degrees of freedom
## Multiple R-squared: 0.8204, Adjusted R-squared: 0.8202
## F-statistic: 3331 on 3 and 2187 DF, p-value: < 2.2e-16Pourquoi n’a t on pas une pente par année ?
lm_eau_air_annee <- lm( T_eau ~ annee_fact + T_air + annee_fact:T_air, data = df_temp)
autoplot(lm_eau_air_annee, data=df_temp)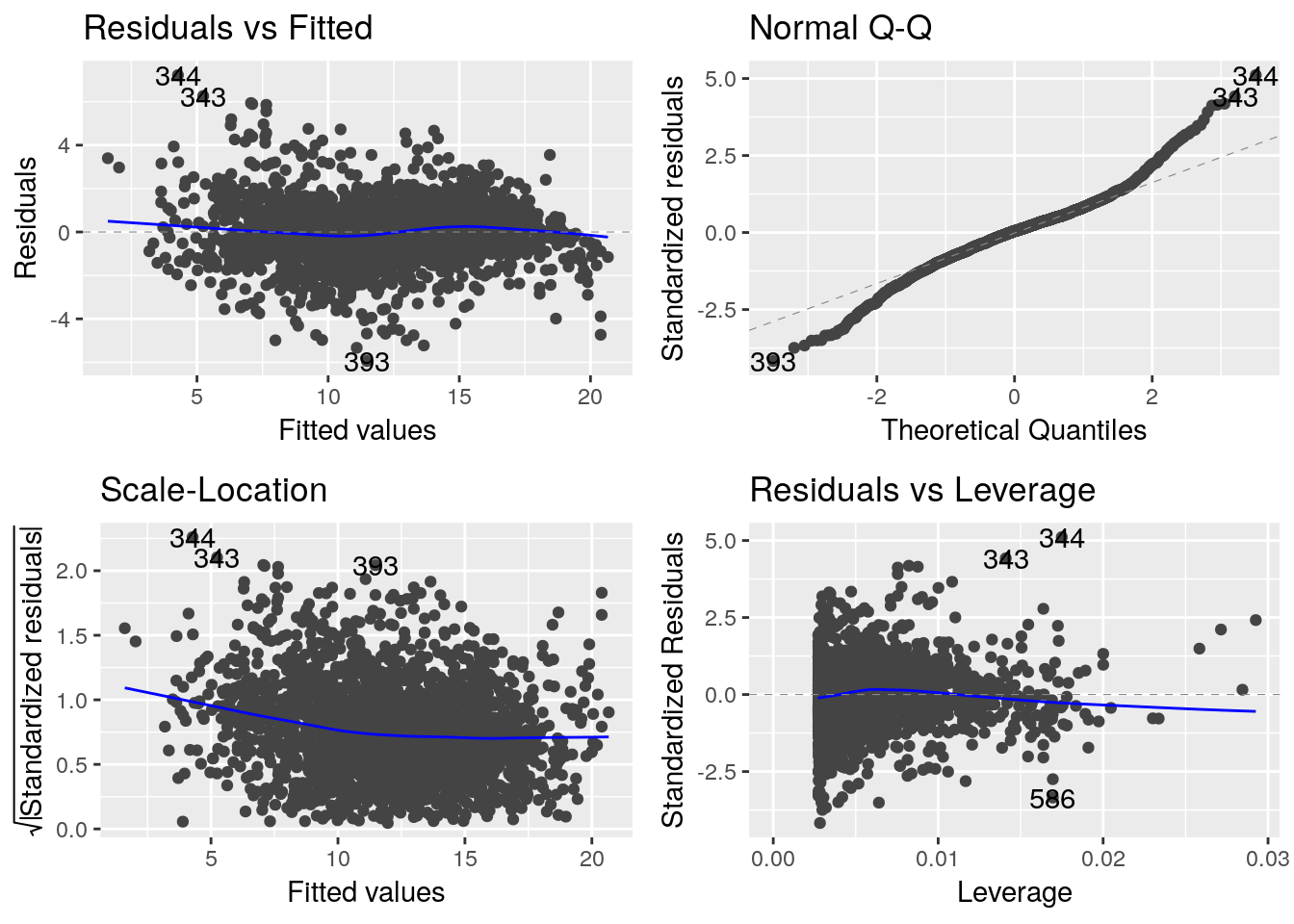
L’analyse des résidus ne contredit pas les hypothèses du modèle.
anova(lm_eau_air_annee)## Analysis of Variance Table
##
## Response: T_eau
## Df Sum Sq Mean Sq F value Pr(>F)
## annee_fact 5 35.3 7.1 3.4692 0.003983 **
## T_air 1 22967.3 22967.3 11287.1529 < 2.2e-16 ***
## annee_fact:T_air 5 378.6 75.7 37.2124 < 2.2e-16 ***
## Residuals 2179 4433.9 2.0
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Anova(lm_eau_air_annee)## Anova Table (Type II tests)
##
## Response: T_eau
## Sum Sq Df F value Pr(>F)
## annee_fact 374.3 5 36.790 < 2.2e-16 ***
## T_air 22967.3 1 11287.153 < 2.2e-16 ***
## annee_fact:T_air 378.6 5 37.212 < 2.2e-16 ***
## Residuals 4433.9 2179
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1summary(lm_eau_air_annee)##
## Call:
## lm(formula = T_eau ~ annee_fact + T_air + annee_fact:T_air, data = df_temp)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.9420 -0.8083 0.0689 0.7628 7.2236
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.84177 0.13847 49.409 < 2e-16 ***
## annee_fact1988 -3.11366 0.23502 -13.249 < 2e-16 ***
## annee_fact1994 -0.87285 0.23588 -3.700 0.000221 ***
## annee_fact1995 -1.96999 0.21485 -9.169 < 2e-16 ***
## annee_fact2001 -1.83219 0.21429 -8.550 < 2e-16 ***
## annee_fact2002 -2.12815 0.25564 -8.325 < 2e-16 ***
## T_air 0.53445 0.01180 45.279 < 2e-16 ***
## annee_fact1988:T_air 0.24044 0.01991 12.076 < 2e-16 ***
## annee_fact1994:T_air -0.01323 0.01903 -0.695 0.487047
## annee_fact1995:T_air 0.07885 0.01739 4.534 6.10e-06 ***
## annee_fact2001:T_air 0.08313 0.01767 4.704 2.71e-06 ***
## annee_fact2002:T_air 0.11075 0.02112 5.245 1.72e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.426 on 2179 degrees of freedom
## Multiple R-squared: 0.8406, Adjusted R-squared: 0.8398
## F-statistic: 1045 on 11 and 2179 DF, p-value: < 2.2e-16La famille des modèles linéaires
Tous les modèles étudiés dans cet exemple font partie de la famille des modèles linéaires.
Le modèle linéaire regroupe tous les modèles pour lesquels le comportement moyen de la variable réponse, i.e. ce qui est prédit par le modèle, est une fonction linéaire des paramètres inconnus. On note souvent \(\hat{y_k}\) la prédiction par le modèle de la k\(^{\mbox{ème}}\) mesure, dans ce cas un modèle linéaire est un modèle tel que \(\hat{y_k}\) est une fonction linéaire des paramètres. Avec cette définition, le modèle \[ Y_k = \alpha + \beta x_k+ \delta x^2_k + E_k, \quad E_k \overset{i.i.d}{\sim}\mathcal{N}(0, \sigma^2),\]
est toujours un modèle linéaire, bien que le lien entre \(y\) et \(x\) ne soit pas linéaire.
Tous les modèles linéaires peuvent être ajustés avec la fonction lm.
Ajustement d’un modèle non linéaire
On s’intéresse maintenant aux données de croissance du fichier data/growth_data.txt.
df_growth <- read.table('data/growth_data.txt', header = TRUE, sep = ' ')
head(df_growth)## age length
## 1 19 36.29889
## 2 12 31.84360
## 3 1 15.77166
## 4 17 33.56730
## 5 38 39.41566
## 6 11 30.48877ggplot(data=df_growth, aes(y=length, x=age)) + geom_point(alpha = 0.3)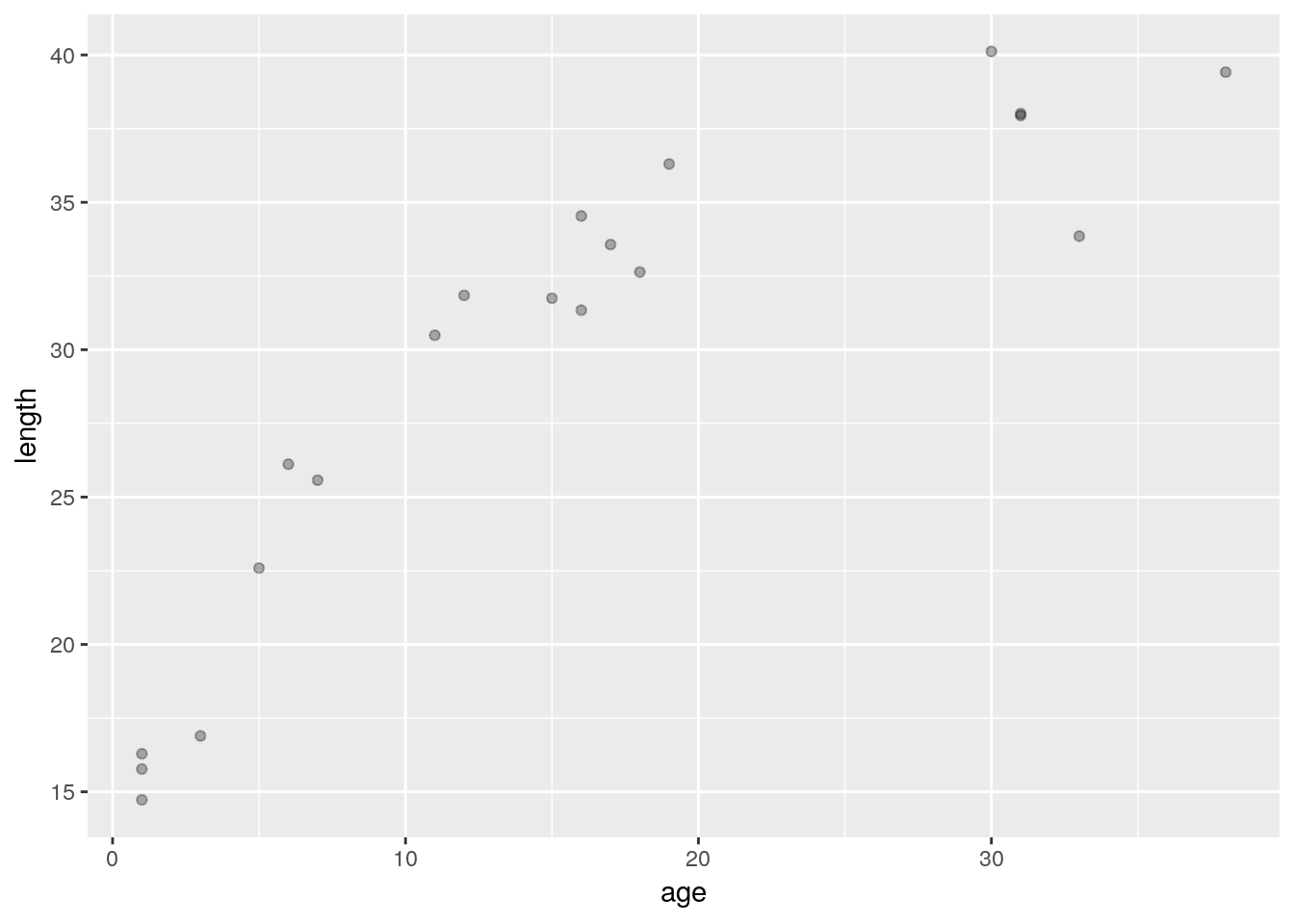
Ajustement d’un modèle linéaire
lm_length_age <- lm( length ~ age, data= df_growth)
autoplot(lm_length_age, data=df_growth)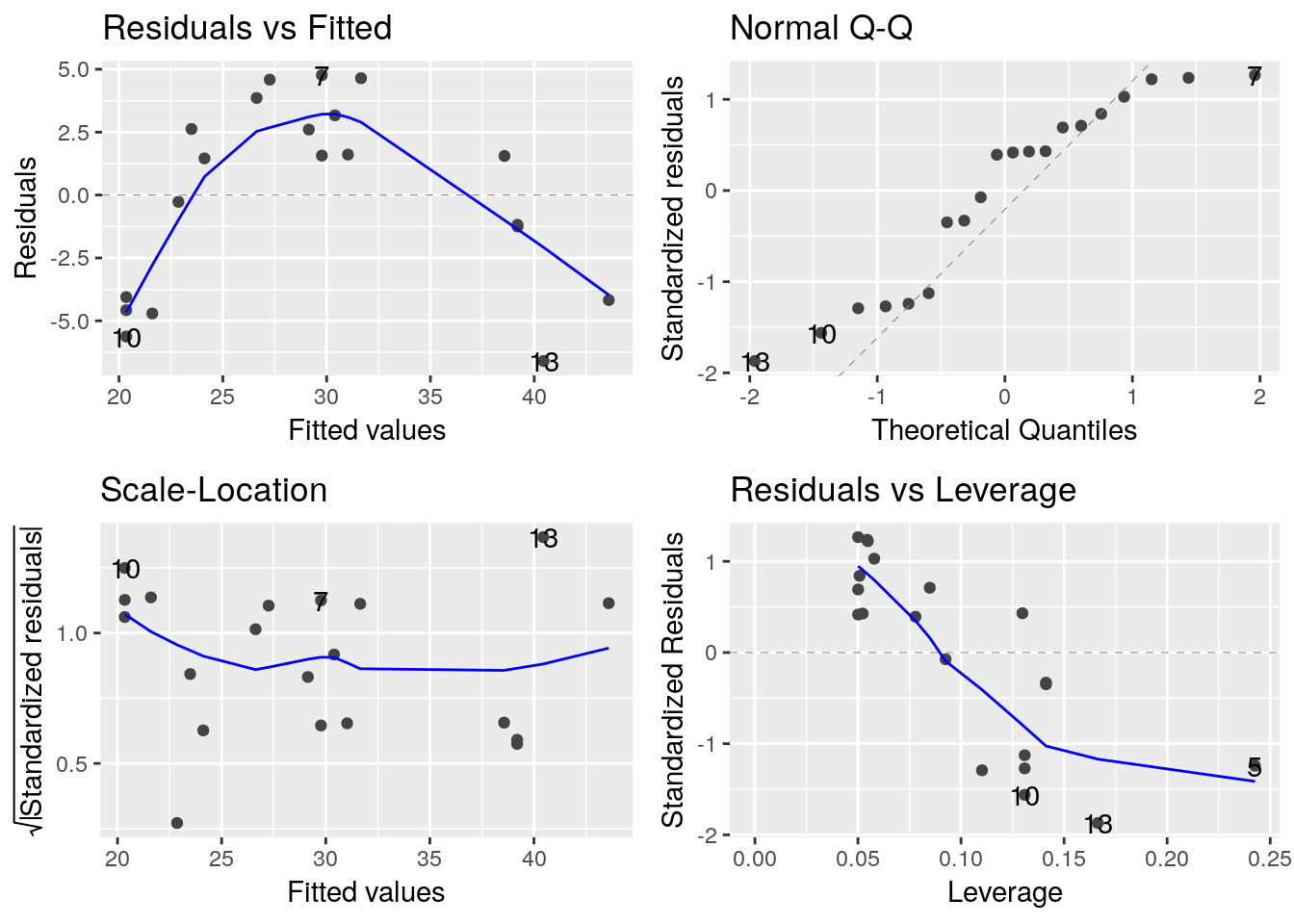
On constate une tendance forte dans les résidus. Le modèle n’est pas adapté; S’agissant de données de croissance, on peut tenter d’ajuster un modèle de von Bertalanffy. Dans ce cas le modèle s’écrit
\[ Y_k = g(x_k) + E_{k}, \quad E_{k} \overset{i.i.d}{\sim}\mathcal{N}(0, \sigma^2),\]
avec - \(Y_k\) la longueur de l’individu \(k\), - \(x_k\) l’âge de lindividu \(k\) - \(g\) la fonction de von Bertalanffy : \(g(x)= L_{\infty} (1-exp(-K*(x-x_0))).\)
func_VonB <- function(x, K, Linf, x0){
res <- Linf*(1-exp(-K*(x-x0)))
return(res)
}Ajustement en utilisant la fonction nls
Pour ajuster cette relation on peut utiliser la fonction nls
## definir des valeurs initiales de parametres
nls_vonB <- nls(length ~ func_VonB(age, K, Linf, x0), start = list(Linf=40,K=1, x0=10), data = df_growth)
summary(nls_vonB)##
## Formula: length ~ func_VonB(age, K, Linf, x0)
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## Linf 38.92930 1.15156 33.806 < 2e-16 ***
## K 0.09638 0.01377 6.999 2.14e-06 ***
## x0 -4.15486 0.84659 -4.908 0.000133 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.701 on 17 degrees of freedom
##
## Number of iterations to convergence: 15
## Achieved convergence tolerance: 9.313e-07Les hypothèses sur les résidus étant les mêmes, il faut les vérifier ‘à la main’.
df_nls_vonB <- df_growth %>% mutate(
fitted = nlsResiduals(nls_vonB)$resi2[,1],
res_stand = nlsResiduals(nls_vonB)$resi2[,2])
ggplot(data = df_nls_vonB, aes(x = fitted, y = res_stand)) + geom_point() + geom_smooth(method = 'loess')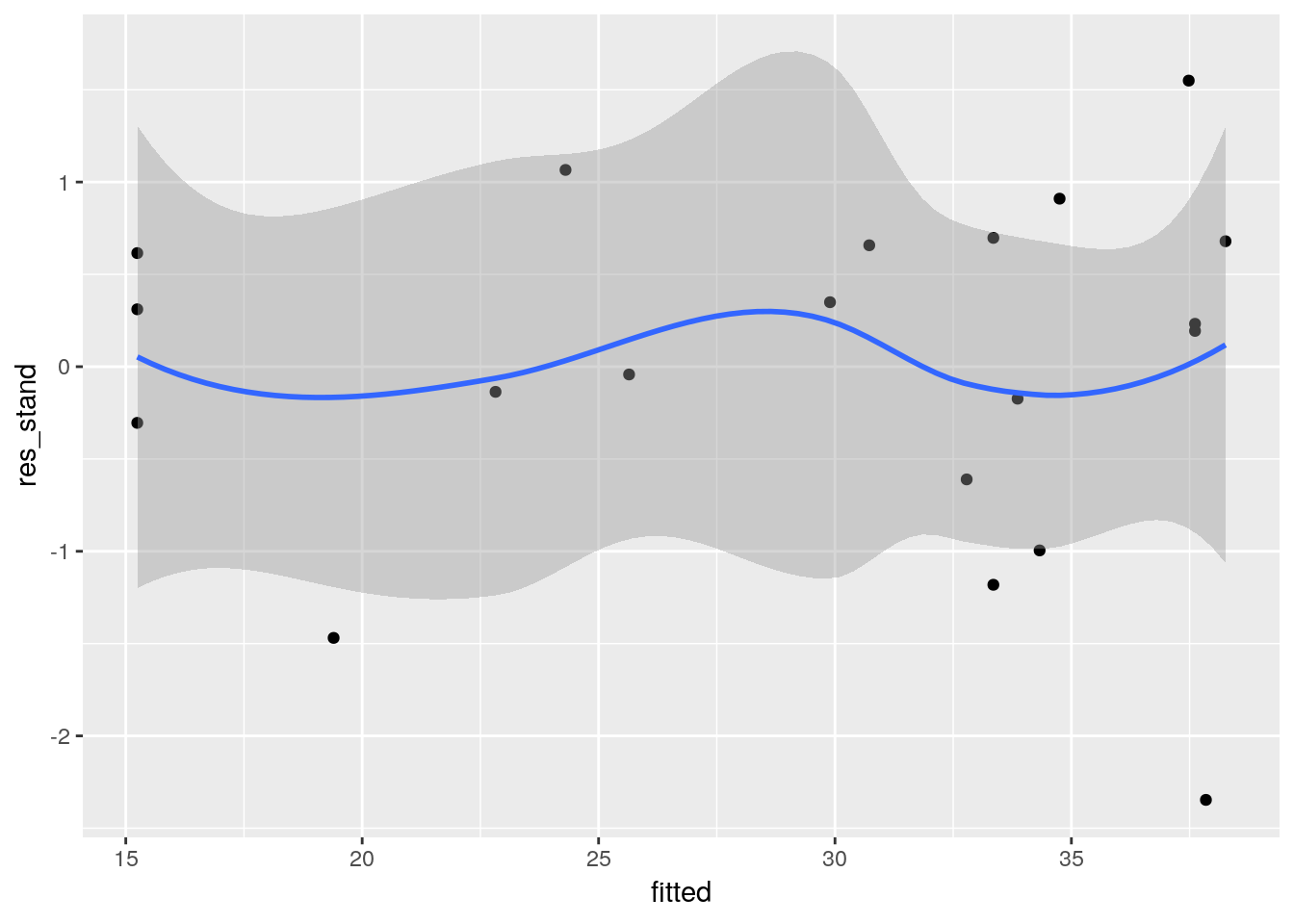
On peut calculer une somme des carrés résiduelle
RSS_1 <- with(df_nls_vonB, sum((length-fitted)^2))
R2_1 <- RSS_1 / with(df_nls_vonB, sum( (length- mean(length))^2) )Mise en oeuvre sur le jeu de données saumons̀
A partir de la table saumons, explorer la variation de la densité en fonction des différents facteurs âge, année, habitat, secteurs, vitesse du courant
Indications :
- Représenter graphiquement les données avant de se lancer dans toute analyse.
- NE PAS PRENDRE EN COMPTE la variable Lf comme variable explicative potentielle.
- Pour la variable « water velocity », on pourra faire des classes.
- Il faudra peut-être transformer la variable si les hypothèses de modélisation ne sont pas vérifiées.
A rendre en binome sous forme de fichier RMarkdown pour le vendredi 14 septembre.