Eléments de correction pour le TD1

Author

Groupes de TD du 15/11

Code 
knitr::opts_chunk$set(echo = TRUE, comment = NA, 
                      cache = TRUE, message = FALSE,
                      warning = FALSE, eval = TRUE,
                      fig.align = "center")

Présentation de Quarto

Quarto permet de faire des rapports intégrant du code R, des sorties exécutées à partir de ce code et du texte présentant les analyses.

Ce document est rédigé avec quarto, le fichier source est disponible sur ce lien

Tip

La documentation officielle de quarto:

https://quarto.org/

Autres docs:

https://www.youtube.com/watch?v=Cwg7tdSdRvY

https://delladata.fr/de-r-markdown-a-quarto/

https://edutechwiki.unige.ch/fr/Quarto

Analyse des caractéristiques géochimiques des sols en forêt de Bornéo

Il s’agit ici de carcatériser les propriétés physico chimiques des sols. Pour ceci on a prélevé des échantillons dans diffférentes forêts de Borneo et on cherche à mettre en évidence des typologies de sols et à identifier des prélèvements qui se ressemblent. Les données consistent en la mesure de caractéristiques géochimiques de sols dans une forêt pluviale de Bornéo.

Comprendre les données

Chargement des packages

Nous utilisons la suite de packages tidyverse pour la manipulation de données, FactomineR pour la mise en oeuvre des analyses factorielles et éventiuellement factoextra pour des sorties plus jolies. (pour une exploration plus interactive on peut utiliser aussi Factoshiny ou explor).

Tip

Une bonne pratique consiste à ne charger que le nombre minimal de packages nécessaires. Evitez de commencer tous les codes avec la même liste de package, pesez l’intérêt de chacun d’eux.

Code 
library(tidyverse)
library(FactoMineR)
library(factoextra)
Tip

Le raccourci pour ajouter un chunk R CTL + Alt + i

Importation

Importation des données

Code 
dta <- read.table(file = "https://marieetienne.github.io/datasets/donnees_sols.txt", sep = ";", header = TRUE)

Description des données

Proposer des résumés univariés de chaque variable présente dans le jeu de données.

Code 
dta  |>    
  summary()
     Sol                Site            Profondeur              pH       
 Length:539         Length:539         Length:539         Min.   :3.400  
 Class :character   Class :character   Class :character   1st Qu.:4.400  
 Mode  :character   Mode  :character   Mode  :character   Median :4.670  
                                                          Mean   :4.632  
                                                          3rd Qu.:4.880  
                                                          Max.   :5.700  
      Eau             Av.P              C                N          
 Min.   :0.170   Min.   : 0.380   Min.   :0.1400   Min.   :0.01000  
 1st Qu.:1.540   1st Qu.: 1.940   1st Qu.:0.5200   1st Qu.:0.05000  
 Median :2.490   Median : 3.160   Median :0.8000   Median :0.07000  
 Mean   :2.698   Mean   : 4.132   Mean   :0.9706   Mean   :0.08056  
 3rd Qu.:3.740   3rd Qu.: 5.235   3rd Qu.:1.2800   3rd Qu.:0.10000  
 Max.   :8.110   Max.   :51.290   Max.   :5.5900   Max.   :0.31000  
      NO3              NH4             Exc.Ac           Exc.Al     
 Min.   : 0.000   Min.   : 0.000   Min.   : 0.250   Min.   :0.030  
 1st Qu.: 0.400   1st Qu.: 1.655   1st Qu.: 1.990   1st Qu.:1.370  
 Median : 1.510   Median : 3.190   Median : 3.420   Median :2.720  
 Mean   : 2.722   Mean   : 5.044   Mean   : 3.781   Mean   :3.151  
 3rd Qu.: 2.965   3rd Qu.: 6.920   3rd Qu.: 5.205   3rd Qu.:4.475  
 Max.   :23.600   Max.   :40.430   Max.   :10.570   Max.   :9.720  
     Exc.Ca            Exc.Mg           Exc.K            Exc.Na       
 Min.   : 0.0000   Min.   :0.0000   Min.   :0.0000   Min.   :0.00000  
 1st Qu.: 0.0400   1st Qu.:0.0700   1st Qu.:0.0500   1st Qu.:0.03000  
 Median : 0.0800   Median :0.2100   Median :0.1100   Median :0.05000  
 Mean   : 0.3029   Mean   :0.6194   Mean   :0.1386   Mean   :0.05237  
 3rd Qu.: 0.1900   3rd Qu.:0.8200   3rd Qu.:0.1700   3rd Qu.:0.07000  
 Max.   :13.4900   Max.   :5.3300   Max.   :1.3000   Max.   :0.27000  
  Exc.Cations        SatBase          Argile          Limon      
 Min.   : 0.380   Min.   : 1.80   Min.   : 8.00   Min.   : 0.00  
 1st Qu.: 2.405   1st Qu.: 7.95   1st Qu.:16.00   1st Qu.:10.00  
 Median : 4.030   Median :13.24   Median :21.00   Median :13.00  
 Mean   : 4.895   Mean   :18.51   Mean   :23.76   Mean   :16.13  
 3rd Qu.: 6.765   3rd Qu.:24.67   3rd Qu.:32.00   3rd Qu.:21.50  
 Max.   :17.300   Max.   :97.54   Max.   :53.00   Max.   :47.00  
     Sable     
 Min.   :15.0  
 1st Qu.:47.0  
 Median :67.0  
 Mean   :60.1  
 3rd Qu.:74.0  
 Max.   :87.0
Note

On remarque que les facteurs sont importés en caractères. transformation de ces variables (Sol,site et Profondeur) en facteur:

Code 
dta <- dta |>    
  mutate(Sol = as.factor(Sol),
         Site = as.factor(Site), 
         Profondeur = as.factor(Profondeur))
dta |>    
  summary()
       Sol            Site             Profondeur        pH       
 Alluvial:180   292-11_A:  3   Intermediaire:180   Min.   :3.400  
 Dunaire :180   292-11_B:  3   Profond      :180   1st Qu.:4.400  
 Grès    :179   292-11_H:  3   Superficiel  :179   Median :4.670  
                292-11_M:  3                       Mean   :4.632  
                292-11_N:  3                       3rd Qu.:4.880  
                292-11_O:  3                       Max.   :5.700  
                (Other) :521                                      
      Eau             Av.P              C                N          
 Min.   :0.170   Min.   : 0.380   Min.   :0.1400   Min.   :0.01000  
 1st Qu.:1.540   1st Qu.: 1.940   1st Qu.:0.5200   1st Qu.:0.05000  
 Median :2.490   Median : 3.160   Median :0.8000   Median :0.07000  
 Mean   :2.698   Mean   : 4.132   Mean   :0.9706   Mean   :0.08056  
 3rd Qu.:3.740   3rd Qu.: 5.235   3rd Qu.:1.2800   3rd Qu.:0.10000  
 Max.   :8.110   Max.   :51.290   Max.   :5.5900   Max.   :0.31000  
                                                                    
      NO3              NH4             Exc.Ac           Exc.Al     
 Min.   : 0.000   Min.   : 0.000   Min.   : 0.250   Min.   :0.030  
 1st Qu.: 0.400   1st Qu.: 1.655   1st Qu.: 1.990   1st Qu.:1.370  
 Median : 1.510   Median : 3.190   Median : 3.420   Median :2.720  
 Mean   : 2.722   Mean   : 5.044   Mean   : 3.781   Mean   :3.151  
 3rd Qu.: 2.965   3rd Qu.: 6.920   3rd Qu.: 5.205   3rd Qu.:4.475  
 Max.   :23.600   Max.   :40.430   Max.   :10.570   Max.   :9.720  
                                                                   
     Exc.Ca            Exc.Mg           Exc.K            Exc.Na       
 Min.   : 0.0000   Min.   :0.0000   Min.   :0.0000   Min.   :0.00000  
 1st Qu.: 0.0400   1st Qu.:0.0700   1st Qu.:0.0500   1st Qu.:0.03000  
 Median : 0.0800   Median :0.2100   Median :0.1100   Median :0.05000  
 Mean   : 0.3029   Mean   :0.6194   Mean   :0.1386   Mean   :0.05237  
 3rd Qu.: 0.1900   3rd Qu.:0.8200   3rd Qu.:0.1700   3rd Qu.:0.07000  
 Max.   :13.4900   Max.   :5.3300   Max.   :1.3000   Max.   :0.27000  
                                                                      
  Exc.Cations        SatBase          Argile          Limon      
 Min.   : 0.380   Min.   : 1.80   Min.   : 8.00   Min.   : 0.00  
 1st Qu.: 2.405   1st Qu.: 7.95   1st Qu.:16.00   1st Qu.:10.00  
 Median : 4.030   Median :13.24   Median :21.00   Median :13.00  
 Mean   : 4.895   Mean   :18.51   Mean   :23.76   Mean   :16.13  
 3rd Qu.: 6.765   3rd Qu.:24.67   3rd Qu.:32.00   3rd Qu.:21.50  
 Max.   :17.300   Max.   :97.54   Max.   :53.00   Max.   :47.00  
                                                                 
     Sable     
 Min.   :15.0  
 1st Qu.:47.0  
 Median :67.0  
 Mean   :60.1  
 3rd Qu.:74.0  
 Max.   :87.0
Code 
# str(dta)
dta <- dta %>% mutate(Sol = as.factor(Sol),
               Site = as.factor(Site),
               Profondeur = factor(Profondeur), levels(c('Superficiel', 'Intermediaire', 'Profond'))) %>% 
  mutate(Profondeur = relevel(Profondeur, ref= "Superficiel"))
 summary(dta)
       Sol            Site             Profondeur        pH       
 Alluvial:180   292-11_A:  3   Superficiel  :179   Min.   :3.400  
 Dunaire :180   292-11_B:  3   Intermediaire:180   1st Qu.:4.400  
 Grès    :179   292-11_H:  3   Profond      :180   Median :4.670  
                292-11_M:  3                       Mean   :4.632  
                292-11_N:  3                       3rd Qu.:4.880  
                292-11_O:  3                       Max.   :5.700  
                (Other) :521                                      
      Eau             Av.P              C                N          
 Min.   :0.170   Min.   : 0.380   Min.   :0.1400   Min.   :0.01000  
 1st Qu.:1.540   1st Qu.: 1.940   1st Qu.:0.5200   1st Qu.:0.05000  
 Median :2.490   Median : 3.160   Median :0.8000   Median :0.07000  
 Mean   :2.698   Mean   : 4.132   Mean   :0.9706   Mean   :0.08056  
 3rd Qu.:3.740   3rd Qu.: 5.235   3rd Qu.:1.2800   3rd Qu.:0.10000  
 Max.   :8.110   Max.   :51.290   Max.   :5.5900   Max.   :0.31000  
                                                                    
      NO3              NH4             Exc.Ac           Exc.Al     
 Min.   : 0.000   Min.   : 0.000   Min.   : 0.250   Min.   :0.030  
 1st Qu.: 0.400   1st Qu.: 1.655   1st Qu.: 1.990   1st Qu.:1.370  
 Median : 1.510   Median : 3.190   Median : 3.420   Median :2.720  
 Mean   : 2.722   Mean   : 5.044   Mean   : 3.781   Mean   :3.151  
 3rd Qu.: 2.965   3rd Qu.: 6.920   3rd Qu.: 5.205   3rd Qu.:4.475  
 Max.   :23.600   Max.   :40.430   Max.   :10.570   Max.   :9.720  
                                                                   
     Exc.Ca            Exc.Mg           Exc.K            Exc.Na       
 Min.   : 0.0000   Min.   :0.0000   Min.   :0.0000   Min.   :0.00000  
 1st Qu.: 0.0400   1st Qu.:0.0700   1st Qu.:0.0500   1st Qu.:0.03000  
 Median : 0.0800   Median :0.2100   Median :0.1100   Median :0.05000  
 Mean   : 0.3029   Mean   :0.6194   Mean   :0.1386   Mean   :0.05237  
 3rd Qu.: 0.1900   3rd Qu.:0.8200   3rd Qu.:0.1700   3rd Qu.:0.07000  
 Max.   :13.4900   Max.   :5.3300   Max.   :1.3000   Max.   :0.27000  
                                                                      
  Exc.Cations        SatBase          Argile          Limon      
 Min.   : 0.380   Min.   : 1.80   Min.   : 8.00   Min.   : 0.00  
 1st Qu.: 2.405   1st Qu.: 7.95   1st Qu.:16.00   1st Qu.:10.00  
 Median : 4.030   Median :13.24   Median :21.00   Median :13.00  
 Mean   : 4.895   Mean   :18.51   Mean   :23.76   Mean   :16.13  
 3rd Qu.: 6.765   3rd Qu.:24.67   3rd Qu.:32.00   3rd Qu.:21.50  
 Max.   :17.300   Max.   :97.54   Max.   :53.00   Max.   :47.00  
                                                                 
     Sable     
 Min.   :15.0  
 1st Qu.:47.0  
 Median :67.0  
 Mean   :60.1  
 3rd Qu.:74.0  
 Max.   :87.0
  • Combien y a t-il de variables quantitatives / qualitatives?
Note

Il y a différentes manières d’identifier le nombre de variables et d’individus. A travers la fonction str() ou sapply(), on a 3 variables qualitatives et 18 variables quantitatives On peut aussi demander le nombre de colonnes et de lignes (ncol, nrow)

Code 
str(dta)
'data.frame':   539 obs. of  21 variables:
 $ Sol        : Factor w/ 3 levels "Alluvial","Dunaire",..: 3 1 1 1 1 1 1 1 1 1 ...
 $ Site       : Factor w/ 180 levels "292-11_A","292-11_B",..: 31 1 1 1 2 2 2 3 3 3 ...
 $ Profondeur : Factor w/ 3 levels "Superficiel",..: 1 1 3 2 1 3 2 1 3 2 ...
 $ pH         : num  4.72 4.56 4.91 4.6 4.67 4.81 4.63 4.84 4.57 4.74 ...
 $ Eau        : num  3.49 2.76 3.39 2.84 3.39 4.28 3.77 4.12 4.98 4.58 ...
 $ Av.P       : num  4.28 7.02 1.75 4.67 4.54 0.7 1.84 4.2 0.88 2.39 ...
 $ C          : num  1.26 0.91 0.3 0.58 0.96 0.38 0.61 0.96 0.47 0.67 ...
 $ N          : num  0.11 0.12 0.06 0.09 0.14 0.08 0.1 0.12 0.08 0.11 ...
 $ NO3        : num  0 10.13 1.84 4.87 1.84 ...
 $ NH4        : num  6.71 2.43 2.17 2.52 3.39 0.66 0.75 3.21 2 2.16 ...
 $ Exc.Ac     : num  4.97 3.96 5.8 5.09 4.14 8.25 6.23 5.48 7.84 6.92 ...
 $ Exc.Al     : num  4.07 3.6 5.33 4.63 3.83 7.65 5.72 4.95 7.68 6.44 ...
 $ Exc.Ca     : num  0.15 0.32 0.15 0.17 0.91 0.2 0.33 1.42 0.3 0.67 ...
 $ Exc.Mg     : num  0.25 0.18 0.2 0.21 0.87 1.2 0.86 1.79 1.98 1.49 ...
 $ Exc.K      : num  0.24 0.21 0.15 0.15 0.16 0.17 0.12 0.22 0.16 0.17 ...
 $ Exc.Na     : num  0.07 0.06 0.05 0.05 0.06 0.06 0.06 0.07 0.06 0.07 ...
 $ Exc.Cations: num  5.68 4.73 6.35 5.68 6.14 ...
 $ SatBase    : num  12.5 16.36 8.69 10.29 32.53 ...
 $ Argile     : int  27 27 31 27 33 43 33 37 45 37 ...
 $ Limon      : int  10 19 16 19 24 26 24 32 25 32 ...
 $ Sable      : int  63 54 52 54 43 31 43 31 30 31 ...
Code 
sapply(dta, class)
        Sol        Site  Profondeur          pH         Eau        Av.P 
   "factor"    "factor"    "factor"   "numeric"   "numeric"   "numeric" 
          C           N         NO3         NH4      Exc.Ac      Exc.Al 
  "numeric"   "numeric"   "numeric"   "numeric"   "numeric"   "numeric" 
     Exc.Ca      Exc.Mg       Exc.K      Exc.Na Exc.Cations     SatBase 
  "numeric"   "numeric"   "numeric"   "numeric"   "numeric"   "numeric" 
     Argile       Limon       Sable 
  "integer"   "integer"   "integer"
Code 
nobs <- nrow(dta)
p <- ncol(dta)
any(is.na(dta))
[1] FALSE
Code 
summary(dta$Profondeur)
  Superficiel Intermediaire       Profond 
          179           180           180

Le fichier de données a 539 lignes et 21colonnes.

Code 
any(is.na(dta))
[1] FALSE
Note

Il n’y a pas de données manquantes.

  • Sont-ils tous prélevés à la même profondeur ?
Note

Observez le site 292-31_D

Code 
dta |> group_by(Site, Profondeur) |> count() 
# A tibble: 539 × 3
# Groups:   Site, Profondeur [539]
   Site     Profondeur        n
   <fct>    <fct>         <int>
 1 292-11_A Superficiel       1
 2 292-11_A Intermediaire     1
 3 292-11_A Profond           1
 4 292-11_B Superficiel       1
 5 292-11_B Intermediaire     1
 6 292-11_B Profond           1
 7 292-11_H Superficiel       1
 8 292-11_H Intermediaire     1
 9 292-11_H Profond           1
10 292-11_M Superficiel       1
# ℹ 529 more rows
  • Quel est le pH moyen tout site/Sol et Profondeur confondu ?
Note

Nous avons le resultat dans le resumé univarié des variables. On peut aussi retrouver via la fonction ci-dessous:

Code 
dta %>% 
  summarise(pH_moyen=mean(pH, na.rm = TRUE))
  pH_moyen
1  4.63154
  • Quelle la variance de la teneur en Eau ? Quelle est la variance de la teneur en Sodium (Na) ?
Code 
dta %>% 
  summarise(var_EAU =var(Eau, na.rm = TRUE),
            var_Sodium =var(Exc.Na, na.rm = TRUE))
  var_EAU  var_Sodium
1 2.11306 0.001288402

Ou de manière générale

Code 
dta |> 
 summarise(across(where(is.numeric), list(moy = mean, var = var))) 
   pH_moy    pH_var  Eau_moy Eau_var Av.P_moy Av.P_var     C_moy     C_var
1 4.63154 0.1419045 2.697607 2.11306 4.131818 12.89734 0.9706122 0.4080084
       N_moy       N_var  NO3_moy  NO3_var  NH4_moy  NH4_var Exc.Ac_moy
1 0.08055659 0.002224225 2.722226 14.09726 5.044249 26.91682   3.781039
  Exc.Ac_var Exc.Al_moy Exc.Al_var Exc.Ca_moy Exc.Ca_var Exc.Mg_moy Exc.Mg_var
1   5.203768   3.151095   4.813158  0.3028757  0.8644495  0.6193692   0.842742
  Exc.K_moy  Exc.K_var Exc.Na_moy  Exc.Na_var Exc.Cations_moy Exc.Cations_var
1 0.1386271 0.01760183 0.05237477 0.001288402        4.894508         10.1526
  SatBase_moy SatBase_var Argile_moy Argile_var Limon_moy Limon_var Sable_moy
1    18.50531    238.9387   23.76438   113.4741  16.12987  72.95708  60.10019
  Sable_var
1  323.3766
Note

La somme des variables Limon, Argile et Sable devrait sommer à 100, mais ce n’est pas le cas à cause des erreurs d’arrondi. Le tableau ci-dessous se lit de la manière suivante. Total représente la somme des proportions exprimée en pourcentage et n le nombre d’observation pour lesquelles la somme des proportion de Limon, Sable et Argil donnent cette valeur.

Code 
count_percent<- dta %>% 
  mutate(Total = Limon + Argile + Sable)  %>% 
  select(Total) |> 
  group_by(Total) |> 
  count()

Représentation bivariée

Pour appréhender le jeu de données, il est utile de commencer par comprendre les relations deux à deux entre les variables. On peut commencer par la corrélation entre celles-ci

Code 
library("corrplot")
dta_quanti <- dta |> 
  select(where(is.numeric))
cor.mat <- round(cor(dta_quanti),2)
corrplot(cor.mat, type="upper", order="hclust", 
         tl.col="black", tl.srt=45)

Code 
cor.mat
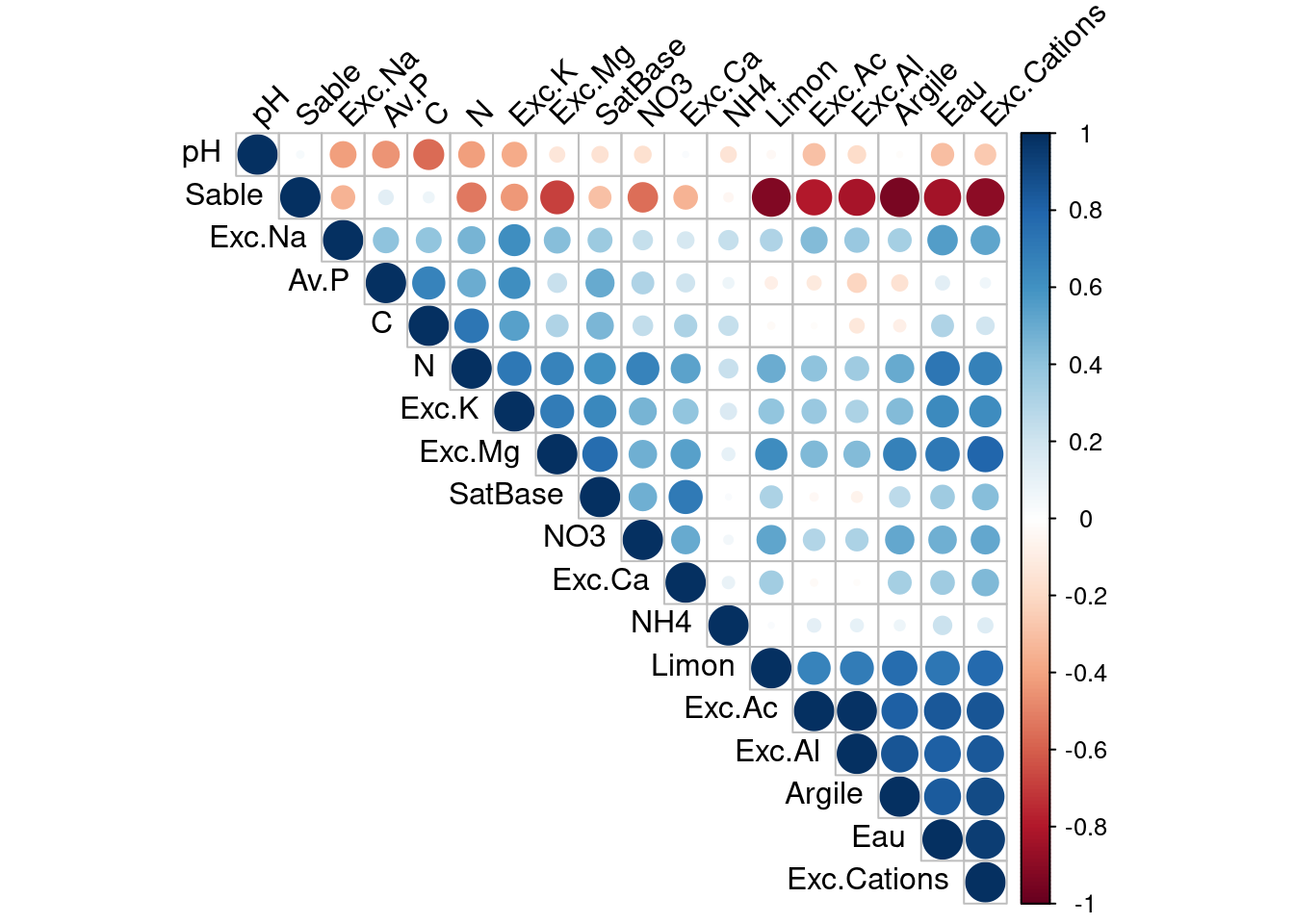
               pH   Eau  Av.P     C     N   NO3   NH4 Exc.Ac Exc.Al Exc.Ca
pH           1.00 -0.31 -0.45 -0.57 -0.42 -0.17 -0.15  -0.30  -0.19   0.02
Eau         -0.31  1.00  0.12  0.30  0.72  0.48  0.21   0.84   0.81   0.35
Av.P        -0.45  0.12  1.00  0.66  0.49  0.30  0.07  -0.12  -0.22   0.20
C           -0.57  0.30  0.66  1.00  0.72  0.24  0.23  -0.02  -0.13   0.31
N           -0.42  0.72  0.49  0.72  1.00  0.66  0.22   0.40   0.35   0.53
NO3         -0.17  0.48  0.30  0.24  0.66  1.00  0.05   0.29   0.31   0.50
NH4         -0.15  0.21  0.07  0.23  0.22  0.05  1.00   0.11   0.10   0.09
Exc.Ac      -0.30  0.84 -0.12 -0.02  0.40  0.29  0.11   1.00   0.98  -0.03
Exc.Al      -0.19  0.81 -0.22 -0.13  0.35  0.31  0.10   0.98   1.00  -0.02
Exc.Ca       0.02  0.35  0.20  0.31  0.53  0.50  0.09  -0.03  -0.02   1.00
Exc.Mg      -0.14  0.71  0.22  0.30  0.66  0.48  0.10   0.44   0.43   0.54
Exc.K       -0.38  0.63  0.61  0.54  0.71  0.46  0.16   0.37   0.31   0.39
Exc.Na      -0.42  0.55  0.40  0.39  0.46  0.23  0.23   0.43   0.37   0.17
Exc.Cations -0.27  0.94  0.06  0.19  0.67  0.51  0.14   0.85   0.84   0.44
SatBase     -0.16  0.35  0.50  0.45  0.60  0.48  0.02  -0.04  -0.07   0.70
Argile      -0.02  0.83 -0.16 -0.09  0.50  0.51  0.07   0.81   0.85   0.33
Limon       -0.04  0.72 -0.09 -0.03  0.49  0.52  0.02   0.66   0.69   0.34
Sable        0.03 -0.84  0.13  0.07 -0.53 -0.55 -0.05  -0.79  -0.83  -0.35
            Exc.Mg Exc.K Exc.Na Exc.Cations SatBase Argile Limon Sable
pH           -0.14 -0.38  -0.42       -0.27   -0.16  -0.02 -0.04  0.03
Eau           0.71  0.63   0.55        0.94    0.35   0.83  0.72 -0.84
Av.P          0.22  0.61   0.40        0.06    0.50  -0.16 -0.09  0.13
C             0.30  0.54   0.39        0.19    0.45  -0.09 -0.03  0.07
N             0.66  0.71   0.46        0.67    0.60   0.50  0.49 -0.53
NO3           0.48  0.46   0.23        0.51    0.48   0.51  0.52 -0.55
NH4           0.10  0.16   0.23        0.14    0.02   0.07  0.02 -0.05
Exc.Ac        0.44  0.37   0.43        0.85   -0.04   0.81  0.66 -0.79
Exc.Al        0.43  0.31   0.37        0.84   -0.07   0.85  0.69 -0.83
Exc.Ca        0.54  0.39   0.17        0.44    0.70   0.33  0.34 -0.35
Exc.Mg        1.00  0.69   0.42        0.79    0.76   0.67  0.62 -0.69
Exc.K         0.69  1.00   0.61        0.62    0.64   0.43  0.39 -0.44
Exc.Na        0.42  0.61   1.00        0.52    0.36   0.33  0.30 -0.34
Exc.Cations   0.79  0.62   0.52        1.00    0.42   0.89  0.77 -0.89
SatBase       0.76  0.64   0.36        0.42    1.00   0.26  0.31 -0.30
Argile        0.67  0.43   0.33        0.89    0.26   1.00  0.76 -0.95
Limon         0.62  0.39   0.30        0.77    0.31   0.76  1.00 -0.92
Sable        -0.69 -0.44  -0.34       -0.89   -0.30  -0.95 -0.92  1.00

En utilisant le package GGallyet notamment la fonction ggpairs, proposer une représentation bivariée des différents couples de variables.

Code 
library(GGally)
ggpairs(dta,  columns = 4:21)

La visualisation est difficile, d’où l’intérêt d’une approche multivariée.

Avant celà , on peut essayer de visualiser le lien entre une variable qualitative (Profondeur ou Type de Sol) et variables quantitatives au travers d’une boîte à moustaches. Par exemple

Code 
dta %>% 
  ggplot() + 
  aes(x= Profondeur, y = Argile) + 
  geom_boxplot() +
  xlab('Classe de Profondeur')

Code 
## ou  boxplot(dta$Argile~ dta$Profondeur)

Approche factorielle

Le but est de faire émerger des typologies de sol. Pour le moment nous mettons de coté les variables qualitatives. Pour visualiser les données on peut commencer par une ACP. l’ACP ne traite que des variables quantitatives, on va considérer les autres variables comme supllémentaires, autrement, dit l’information qu’elles contiennent ne contribuent pa sà la définition des axes.

Pour faire le lien avec le cours on va définir les objets du cours dans le cadre de cet exercice. La matrice des données est \(X\).

Code 
X <- dta %>% 
  select(where(is.numeric)) %>% as.matrix()
dim(X)
[1] 539  18

Mise en place de l’approche factorielle

  • Comment décider le poids attribuer à chaque individu ?
Note

Par défaut le poids est 1/n sauf si autre bonne raison

Les poids sont stockés dans la matrice \(W\)

Code 
W <- diag(1/nobs, ncol = nobs, nrow = nobs)
dim(W)
[1] 539 539

Distance à utiliser entre les individus

Si on considère une distance euclidienne, la matrice de distance \(M\) est l’identité.

Code 
p_quanti <- ncol(X)
M <- diag(1, ncol = p_quanti, nrow = p_quanti)
dim(M)
[1] 18 18

Le cours dit que si \(X\) est cebtrée alors l’inertie vaut \(tr(X^\top W X M)\)

Pour vérifier on va définir la matrice \(X\) centrée et calculer l’inertie à l’aide de la formule du cours. La fonction tr n’est pas disponible dans R par défaut

Code 
tr <- function(X){
  sum(diag(X))}
Code 
X_center <- dta |> select(where(is.numeric))  |> scale(center = TRUE, scale = FALSE) 
inertie <- tr(t(X_center) %*% W %*% X_center %*% M)

L’inertie vaut 825.6839644.

Les axes principaux seront les vecteurs propres et l’inertie portée par chaque axe, sera la valeur propre associée

Code 
VM  <- t(X_center) %*% W %*% X_center %*% M
inertia_dec <- eigen(VM)$values

pour faire une ACP non normée dans R, on utilise la fonction PCAde FactomineR, en précisant l’option scale=FALSE pour indiquer que l’on veut un ACP non normée

Note

Par défaut la fonction PCA fait une ACP normée !!

Code 
dta_pca <- PCA(X = dta, scale.unit = FALSE, 
               quali.sup = c(1,2,3), ncp = 18)
#library(Factoshiny)

Si on fait une ACP non normée, on constate que le Sable et SatBase contribuent beaucoup plus à la formation des axes que les autres variables. EN effet dans une ACP non normée, l’information (= l’inertie) portée par une variable est la variance de cette variable . Les variances des variables (ordonnées par ordre décroissant) sont rappelées ci-dessous :

Code 
ordered_variance <- dta |> 
  summarise(across(where(is.numeric), ~var(.x)*(nobs-1)/nobs)) |> 
   pivot_longer( cols = everything(), names_to = "Variable", values_to = "Variance") |> 
  mutate(Variance = round(Variance, 2)) |> 
  arrange(-Variance)
ordered_variance 
# A tibble: 18 × 2
   Variable    Variance
   <chr>          <dbl>
 1 Sable         323.  
 2 SatBase       238.  
 3 Argile        113.  
 4 Limon          72.8 
 5 NH4            26.9 
 6 NO3            14.1 
 7 Av.P           12.9 
 8 Exc.Cations    10.1 
 9 Exc.Ac          5.19
10 Exc.Al          4.8 
11 Eau             2.11
12 Exc.Ca          0.86
13 Exc.Mg          0.84
14 C               0.41
15 pH              0.14
16 Exc.K           0.02
17 N               0   
18 Exc.Na          0
Note

Ainsi, puisque les variances des variables Sable et SatBase (et dans une moindre mesure Argile et Limon) sont très grandes devant les autres, ces variables contribuent davantage à la formation des premiers axes. Pour bien comprendre, il faut se rendre compte qu’en résumant le jeu de données aux seules variables Sable et SatBase, on représente déjà un pourcentage d’inertie de 67.98.

Pour voir comment l’information d’une variable se disperse sur les différentes dimensions on peut regarder la contribution de cette variable à la construction des différents axes.

Par exemple pour le Sable et le pH.

Code 
round(dta_pca$var$contrib[c("Sable", "pH" ),],2)
      Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7 Dim.8 Dim.9 Dim.10 Dim.11
Sable 56.42  6.92  0.21  0.66  0.09  0.01  2.19  0.01  0.00   0.01   0.09
pH     0.00  0.00  0.02  0.00  0.21  0.25  0.91  0.11  1.13   2.78  26.47
      Dim.12 Dim.13 Dim.14 Dim.15 Dim.16 Dim.17 Dim.18
Sable  33.31   0.02   0.05   0.01      0      0      0
pH      0.31  57.55  10.24   0.02      0      0      0
Important

Si vos données sont toutes dans la même unité de mesure et varient dans des gammes de valeurs identiques: l’ACP non-normée est souvent recommandée.

Si vos données sont dans des unités de mesure différentes et varient dans des gammes de valeurs différentes: l’ACP normée est recommandée

l’ACP non normée est basée sur la matrice de covariances, qui se calcule par \(VM =t(X) W W M\), avec \(M\) la matrice identité.

l’ACP normée est basée sur la matrice de corrélations, qui se calcule par \(VM =t(X) W W M\), mais avec \(M\) la matrice diagnonale dont chaque terme diagonale est l’inverse de la variance de la variable concernée

Ici les variables ont des ordres de grandeur différent, la mesure de pH n’est pas comparable avec la teneur en Sodium par exemple, on va faire une ACP normée, on propose donc d’équilibrer le poids des variables dans la construction des projections en proposant une ACP normée. Mais avant de passer à cette ACP non normée, on peut vérifier que les vecteurs propres obtenus “à la main# coincident avec les vecteurs propres obtenus par la fonction PCA. On le vérifier sur les deux premiers axes. Pour le vérifier on divise terme à terme chaque terme du vecteur propre obtenu avec PCA par le terme correspondant obtenu à la main.

Code 
dta_pca$svd$V[,1:2] / eigen(VM)$vectors[,1:2 ]
      [,1] [,2]
 [1,]    1   -1
 [2,]    1   -1
 [3,]    1   -1
 [4,]    1   -1
 [5,]    1   -1
 [6,]    1   -1
 [7,]    1   -1
 [8,]    1   -1
 [9,]    1   -1
[10,]    1   -1
[11,]    1   -1
[12,]    1   -1
[13,]    1   -1
[14,]    1   -1
[15,]    1   -1
[16,]    1   -1
[17,]    1   -1
[18,]    1   -1

ACP normée

  • Quelles variables choisissez-vous de considérer comme supplémentaires (qualitative et ou quantitative) ?
Note

Les variables illustratives ou supplémntaires n’interviennent pas pour la construction des composantes ou axes. Elles sont utilisées après coup pour mieux comprendre / commenter les résultats. Des individus peuvent aussi être traités comme illustratifs.

Dans notre exemple, seules les variables qualitatives sont choisies en supplémentaires.

  • Quelle doit être l’inertie du nuage ?
Note

Dans une ACP normée, la somme des valeurs propres est égale au nombre de variables.

On peut à nouveau le vérifier à la main. Le cours dit que si \(X\) est cebtrée alors l’inertie vaut $tr(X^W X M), $ cette fois \(M\) est la matrice diagonale contenant l’inverse des variances.

Code 
p_quanti <- ncol(X)
variance <- dta_quanti |> 
  summarise(across(where(is.numeric), ~var(.x)*(nobs-1)/nobs)) |> 
   pivot_longer( cols = everything(), names_to = "Variable", values_to = "Variance") |> 
  pull(Variance)
M_norm <- diag(1/variance, ncol = p_quanti, nrow = p_quanti)
dim(M_norm)
[1] 18 18
Code 
VM_norm <- t(X_center) %*% W %*% X_center %*% M_norm
inertie_norm <- tr(VM_norm)

L’inertie dans l’ACP normée vaut 18.

Pour finir l’ACP “à la main”, on peut voir que l’on pourrait toutes les informations pertinentes à partir de la seule étude de la matrice de la corrélation
Par exemple, l’éboulis des valeurs propres.

  • A l’aide de la fonction eigen représenter la suite décroissante des valeurs propres. A partir de combien de vecteurs de base considérez-vous que l’information apportée devient négligeable?
Code 
## Verifier que  Cor(data) = t(X_reduit) %*% W %*% X_reduit
X_reduit <- X_center %*% sqrt(M)
correlation_mat <- t(X_reduit) %*% W %*% X_reduit
max(abs(cor(dta_quanti)-correlation_mat))
[1] 321.7766
Code 
Cor_eigen <- eigen(correlation_mat)
valeurspropres <- Cor_eigen$values
vecteurspropres <- Cor_eigen$vectors
dta.vp <- data.frame(index = 1:length(valeurspropres), valeurspropres = valeurspropres, inertiepercent = cumsum(valeurspropres)/sum(valeurspropres))
dta.vp
   index valeurspropres inertiepercent
1      1   5.459321e+02      0.6611877
2      2   2.093213e+02      0.9147004
3      3   2.772075e+01      0.9482734
4      4   2.138866e+01      0.9741776
5      5   1.070946e+01      0.9871480
6      6   6.876714e+00      0.9954765
7      7   2.355919e+00      0.9983298
8      8   6.460148e-01      0.9991122
9      9   2.708809e-01      0.9994403
10    10   1.789621e-01      0.9996570
11    11   1.128154e-01      0.9997937
12    12   8.284054e-02      0.9998940
13    13   5.151668e-02      0.9999564
14    14   2.953466e-02      0.9999921
15    15   5.594256e-03      0.9999989
16    16   6.983405e-04      0.9999998
17    17   1.825201e-04      1.0000000
18    18   7.816816e-06      1.0000000
Code 
dta.vp |> 
  mutate(diffinertie = valeurspropres-lead(valeurspropres))
   index valeurspropres inertiepercent  diffinertie
1      1   5.459321e+02      0.6611877 3.366108e+02
2      2   2.093213e+02      0.9147004 1.816006e+02
3      3   2.772075e+01      0.9482734 6.332085e+00
4      4   2.138866e+01      0.9741776 1.067920e+01
5      5   1.070946e+01      0.9871480 3.832751e+00
6      6   6.876714e+00      0.9954765 4.520795e+00
7      7   2.355919e+00      0.9983298 1.709904e+00
8      8   6.460148e-01      0.9991122 3.751339e-01
9      9   2.708809e-01      0.9994403 9.191881e-02
10    10   1.789621e-01      0.9996570 6.614671e-02
11    11   1.128154e-01      0.9997937 2.997485e-02
12    12   8.284054e-02      0.9998940 3.132386e-02
13    13   5.151668e-02      0.9999564 2.198201e-02
14    14   2.953466e-02      0.9999921 2.394041e-02
15    15   5.594256e-03      0.9999989 4.895915e-03
16    16   6.983405e-04      0.9999998 5.158204e-04
17    17   1.825201e-04      1.0000000 1.747033e-04
18    18   7.816816e-06      1.0000000           NA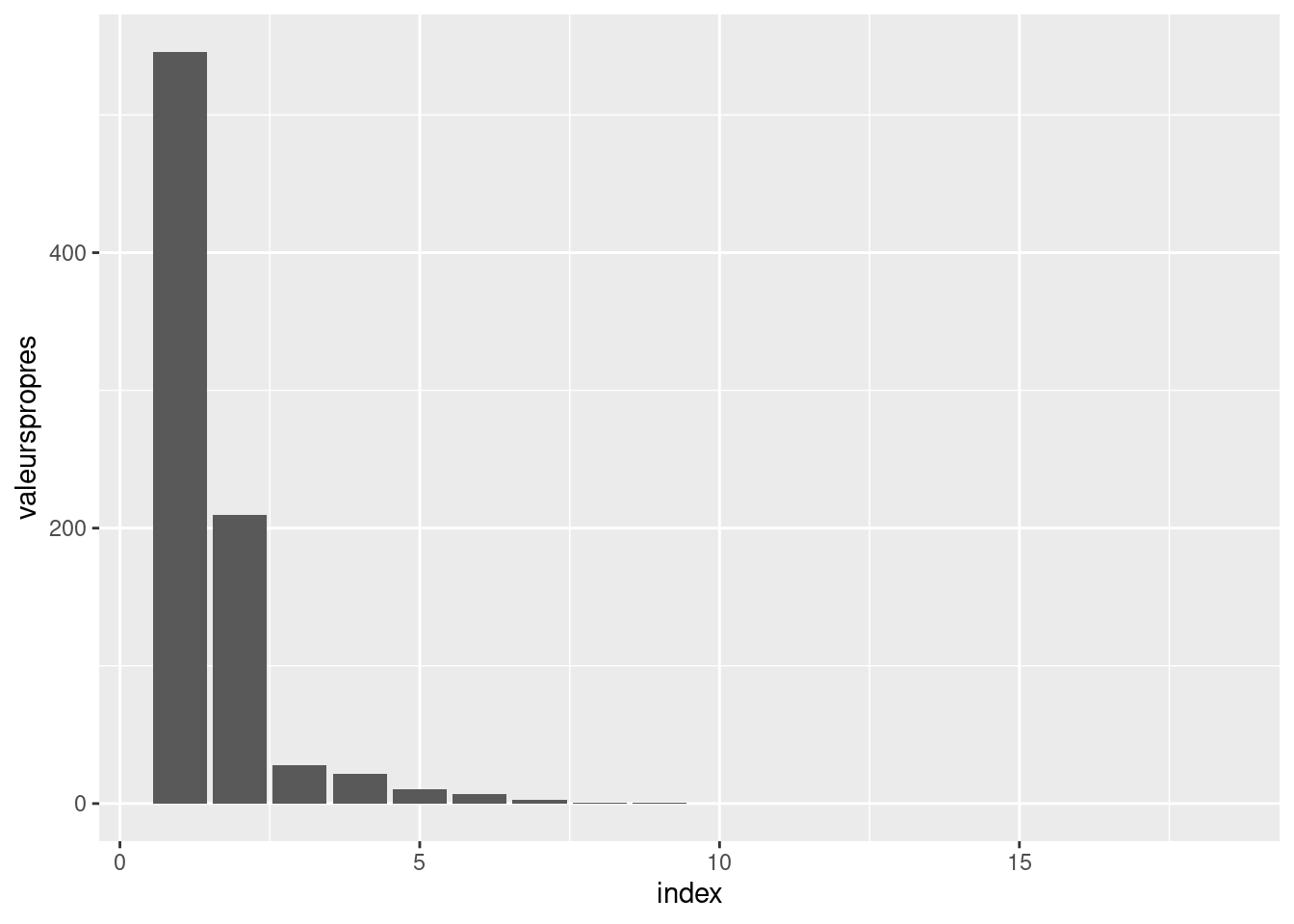
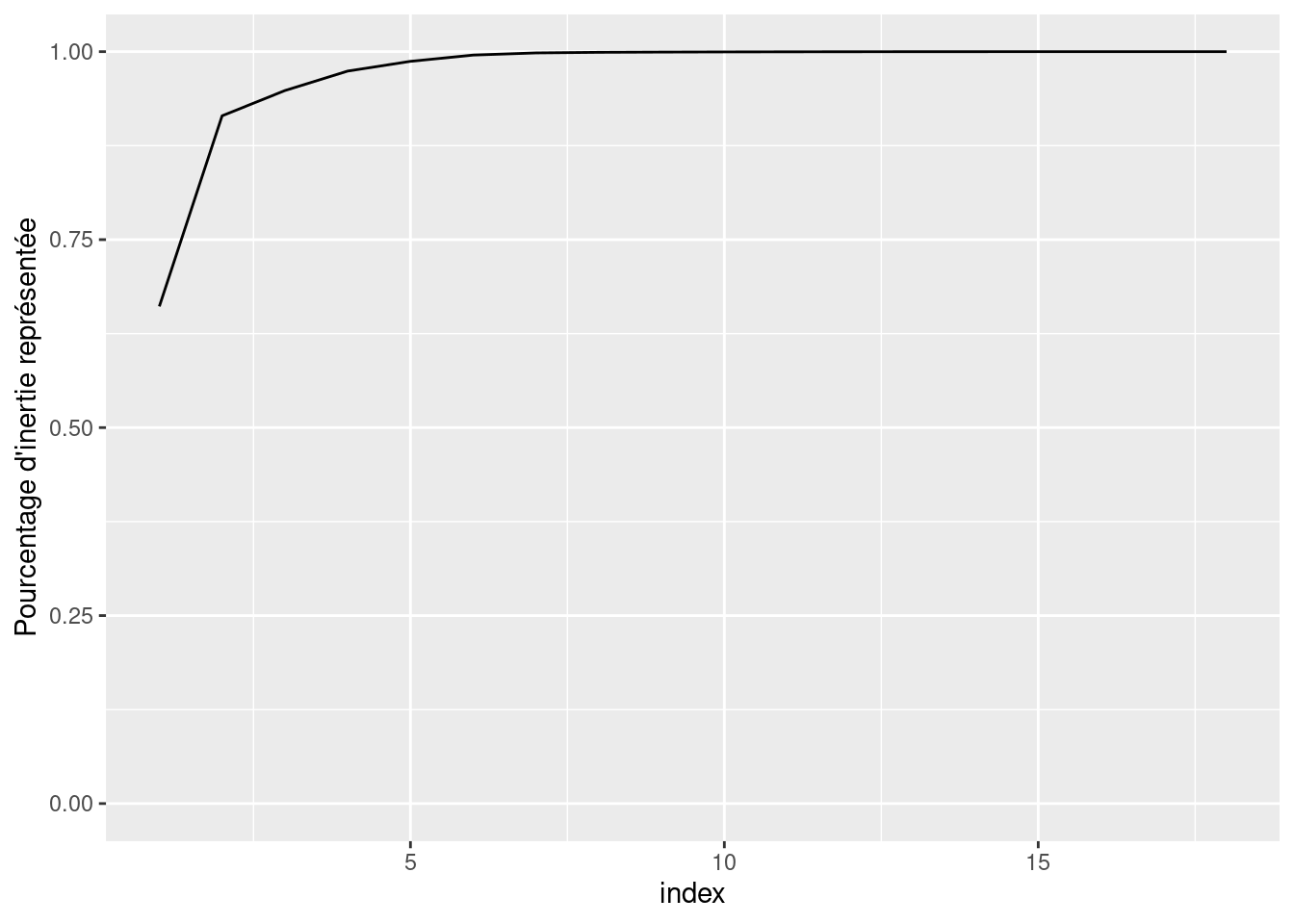
Code 
#lead est une fonction positionnelle. elle
# permet d'accèder à une valeur stockée dans une ligne inférieure: elle décale d'un rang le vecteur. le 2eme élément devient le 1er et le 3eme devient le 2eme et ainsi de suite 
dta.vp  |> ggplot() +  geom_col(aes(x=index, y = valeurspropres))

Code 
dta.vp  |> ggplot() +  geom_line(aes(x=index, y = inertiepercent)) + ylim(c(0,1)) + ylab("Pourcentage d'inertie représentée")

On peut maintenant mettre en place une ACP normée, avec factomineR et en utilisant et factoextra pour des sorties plus agréables. On précise que l’ACP est normée grace à l’option scale.unit = TRUE.

Code 
dta_pca <- PCA(X = dta, scale.unit = TRUE, quali.sup = c(1,2,3), ncp = 18, graph = FALSE)
#library(Factoshiny)
Note

le champs eig de l’objet dta_pcacontient les informations sur les valeurs propres

On peut notamment s’intéresser à la qualité globale des représentations

  • sur le plan 1-2 : on représente 66.9241274

  • sur le plan 1-3 : on représente 57.5578374

  • Représentez l’éboulis des valeurs propres à partir de la sortie dta_pca (ce qui a déjà été fait à la main précédemment).

Code 
dta_pca$eig |> 
  as.data.frame() |>  
  rowid_to_column() |> 
  ggplot() + geom_col(aes(x=rowid, y =eigenvalue))

  • A partir de combien d’axes factoriels considérez-vous que l’information apportée devient négligeable?
Important

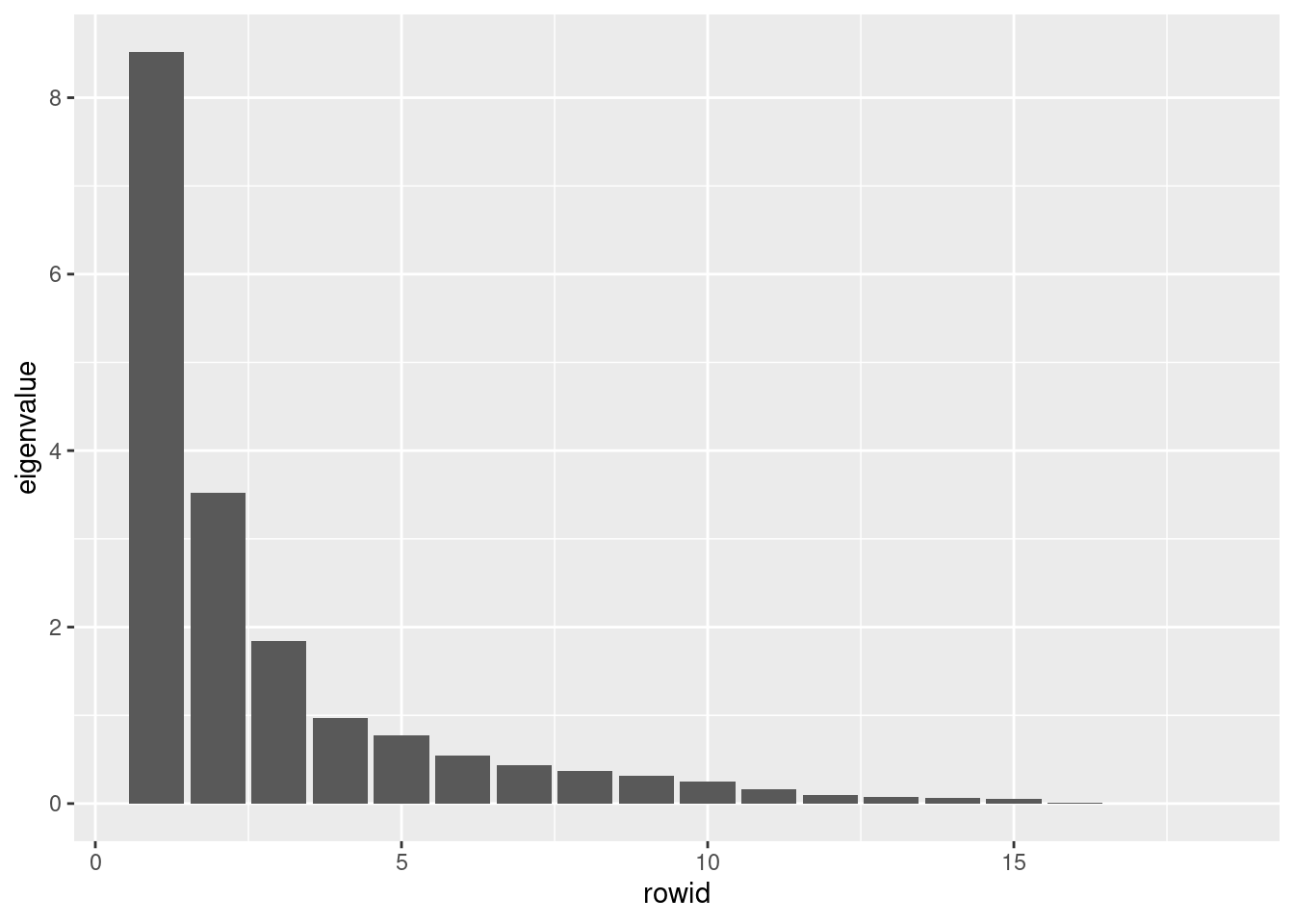
Il existe plusieurs “règles” ce qui est le signe qu’il n’y a pas une seule façon de faire mais des guides

Règle de l’ébouli des valeurs propres: garder les axes correspondant aux valeurs propres situées avant le point d’inflexion (cassure, coude) sur le graphes des valeurs propres.

Règle de Kaiser: garder les axes correspondant aux valeurs propres supérieures à la moyenne des valeurs propres:

  • supérieures à 1 en ACP normée

  • supeérieur à Inertie/p en ACP non normée

Règle empirique: garder les facteurs expliquant un pourcentage de variance cumulée satisfaisant (géneralement 80%)

Dans notre exemple, avec 3 axes on représente 77.1397764 de l’inertie, l’axe 4 est proche de la valeur moyenne d’inertie.

Tout nous incite à regarder les 3 et éventuellement 4 premiers axes.

Variables

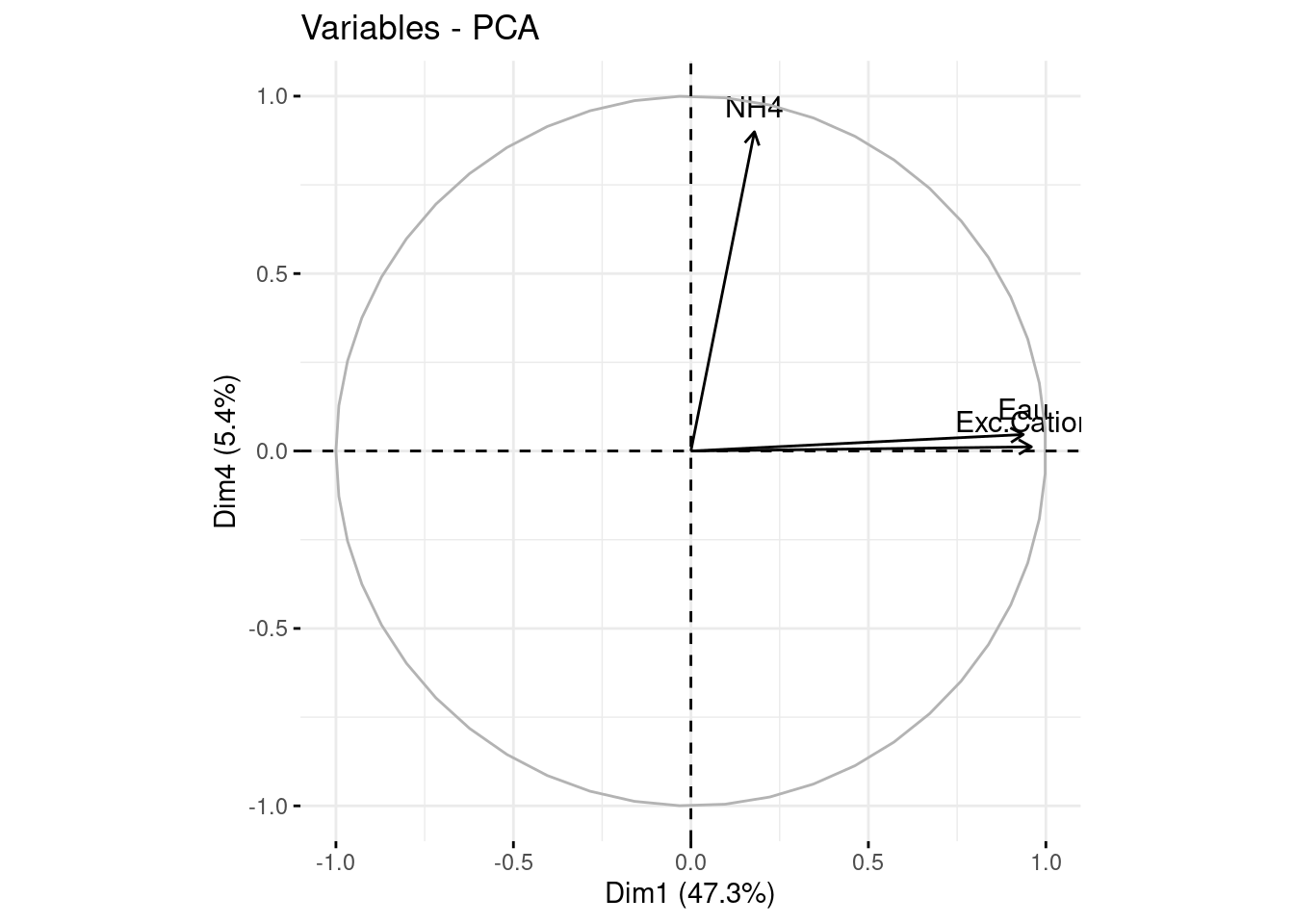
On peut visualiser le cercle des corrélations

Le package factoextradonne des outils pour produire des sorties les plus lisibles possibles.

Pour représenter le cercle des corrélations dans un plan principal, on utilise la fonction fviz_pca_var. Sur chaque graphe, qu’est ce qui est représenté?

Code 
fviz_pca_var(dta_pca,
             axes = c(1, 2)) # Numéro des axes à représenter

Code 
fviz_pca_var(dta_pca,
             axes = c(1, 3)) #

Code 
fviz_pca_var(dta_pca,
             axes = c(2, 3)) #

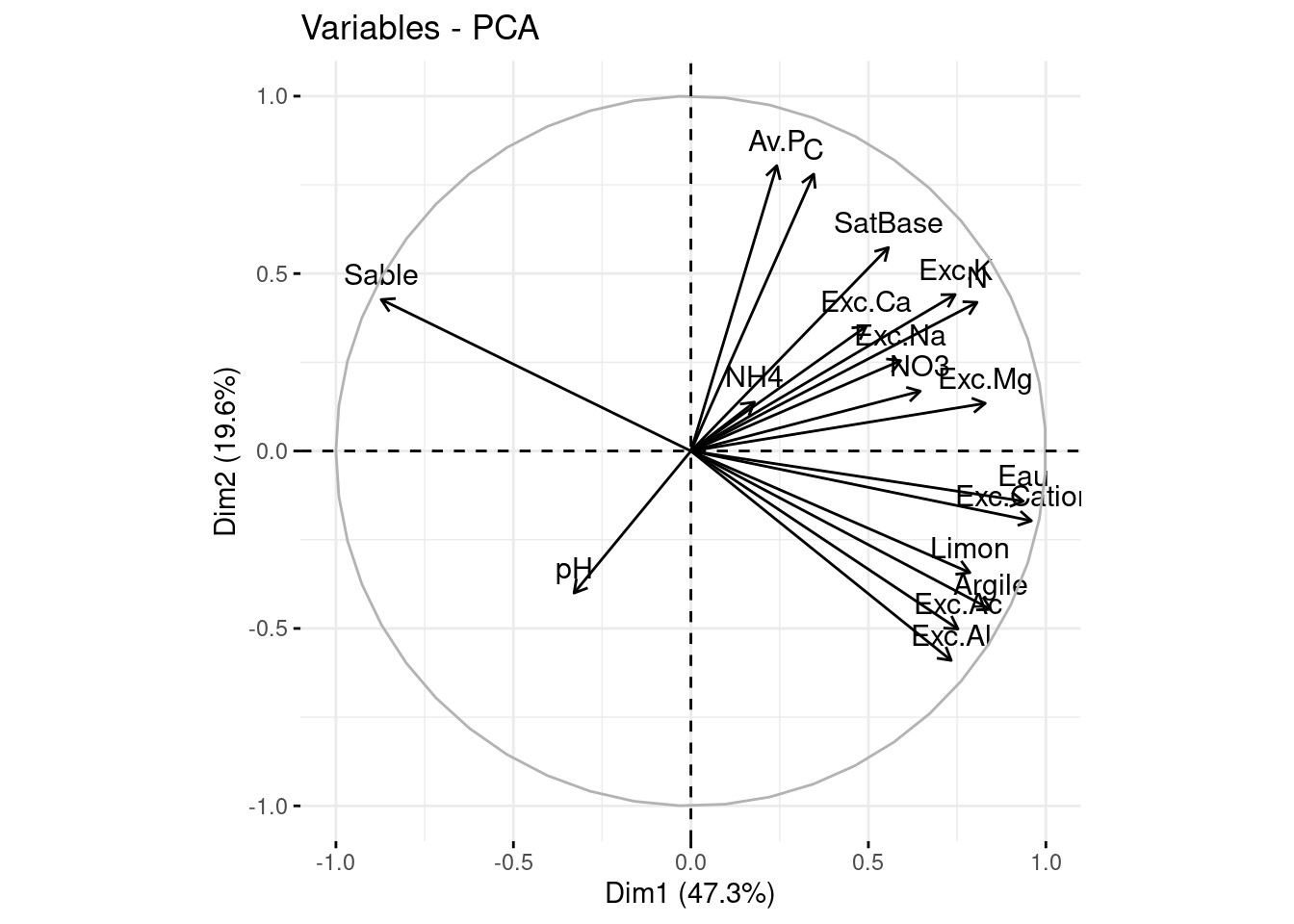
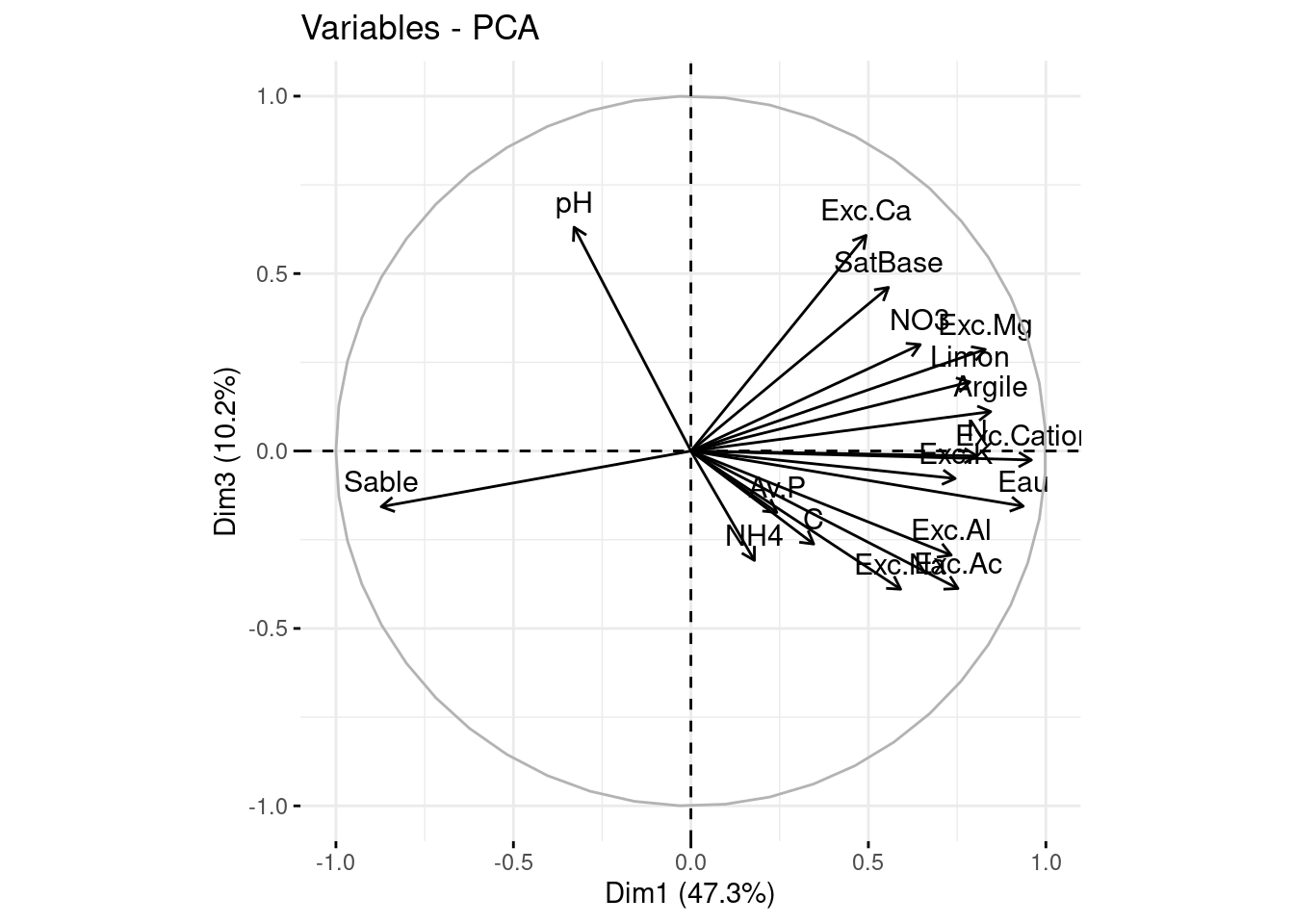
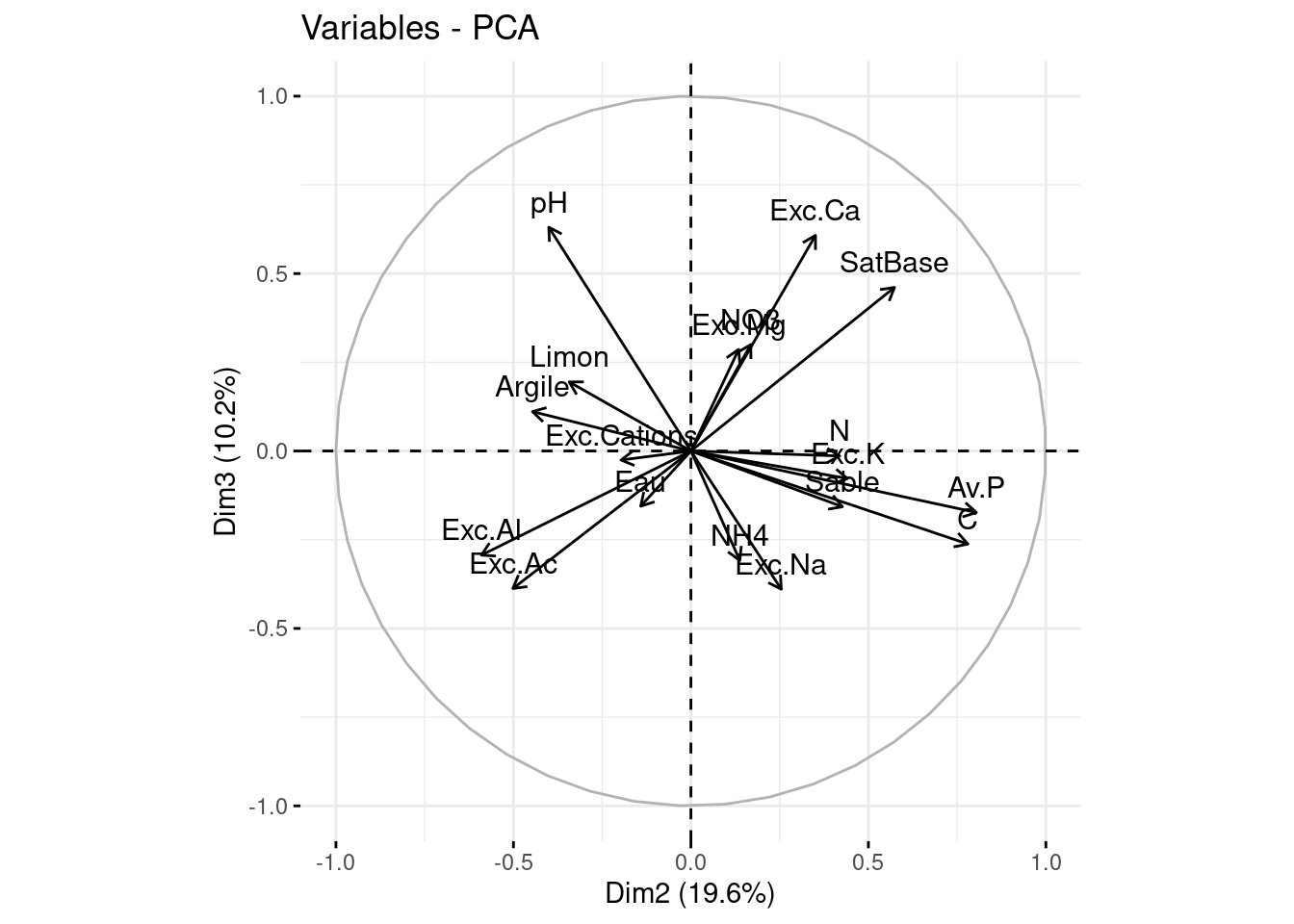
Pour plus de lisibilité, refaites le même graphique avec seulement les variables bien représentées (par exemple celles pour lesquelles le cos2 de l’angle entre la variable initiale et la variable projetée dans le plan représenté est supérieure à 0.8 ou 0.6 selon les cas). Jouer sur les différentes repésentations pour bien comprendre quelle information est disponible sur chaque projection, on peut arranger les graphiques les uns à coté des autres pour une visualisation plus commode.

Code 
pplotvar_12 <- fviz_pca_var(dta_pca,
             axes = c(1, 2), 
             select.var = list(cos2 = 0.8)) # Numéro des axes à représenter 
pplotvar_13 <- fviz_pca_var(dta_pca,
             axes = c(1, 3), 
             select.var = list(cos2 = 0.8)) #
pplotvar_23 <- fviz_pca_var(dta_pca,
             axes = c(2, 3), 
             select.var = list(cos2 = 0.6)) # 

## si on ne veut pas importer tout un package, on peut indiquer qu'on utilise la fonction ggarrange du package ggpur avec la synthaxe suivante
## on exécute le code uniquement si le package est est installé
if("ggpubr" %in% installed.packages()[,1]){
  ggpubr::ggarrange( pplotvar_12 + labs(caption = 'select cos2 > 0.8'), 
                     NULL, 
                     pplotvar_13 + labs(caption = 'select cos2 > 0.8'),  
                     pplotvar_23 + labs(caption = 'select cos2 > 0.6'),
                     ncol = 2, nrow = 2)
}

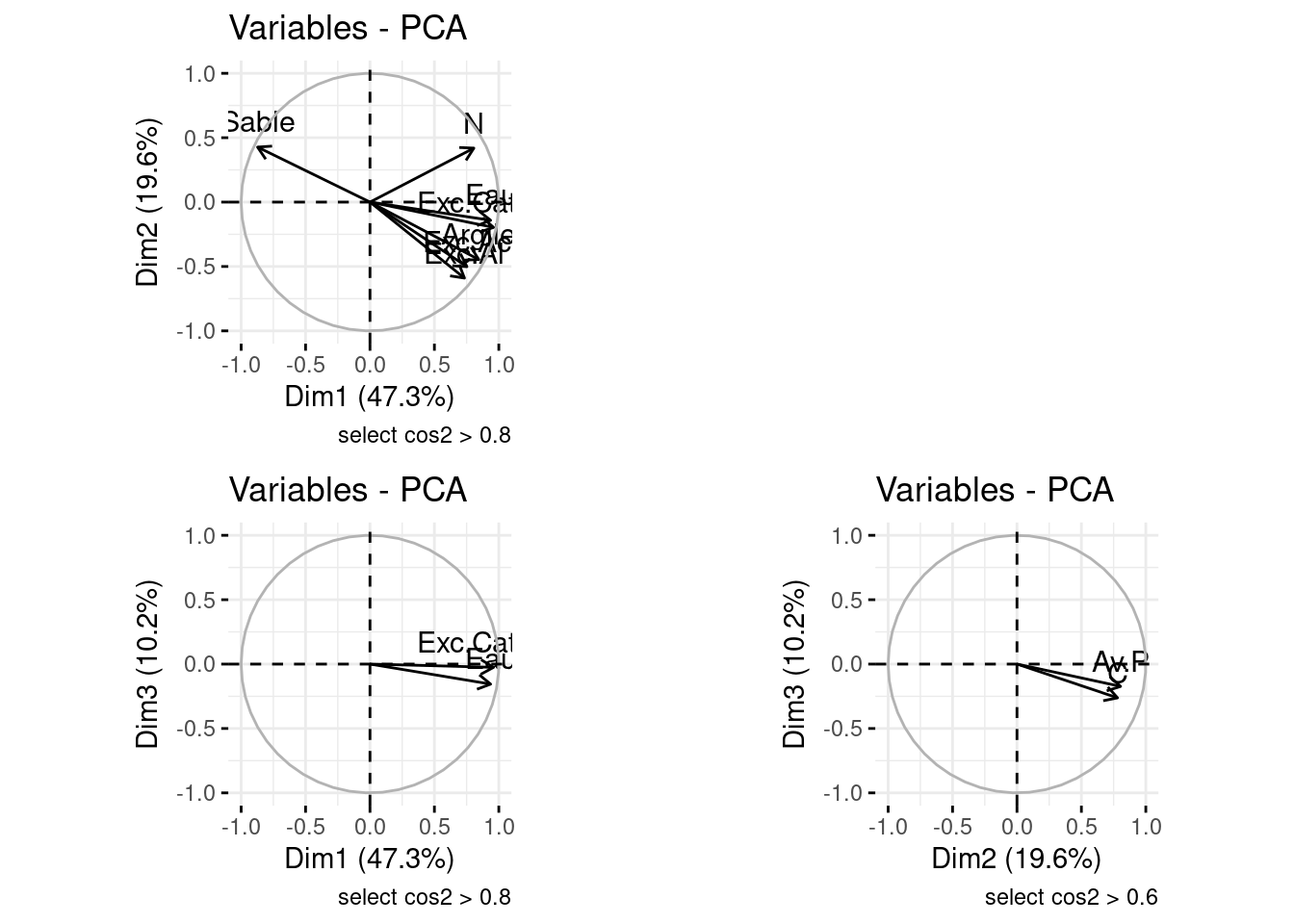
Il est important de noter qu’on peut grâce à dta_acp, tracer ce graphique nous même et donc modifier son apparence à notre guise. Par ailleurs les fonction de factoextra renvoie des objets de type ggplot que l’on peut aisément modifier. (aucune excuse pour les graphiques laids !)

On se posait la question de l’intérêt d’aller voir l’axe 4, la visualisation ci-dessous nous montre que l’axe 4 porte essentiellement l’information sur NH4.

Code 
pplotvar_14 <- fviz_pca_var(dta_pca,
             axes = c(1, 4), 
             select.var = list(cos2 = 0.8)) # 
pplotvar_14

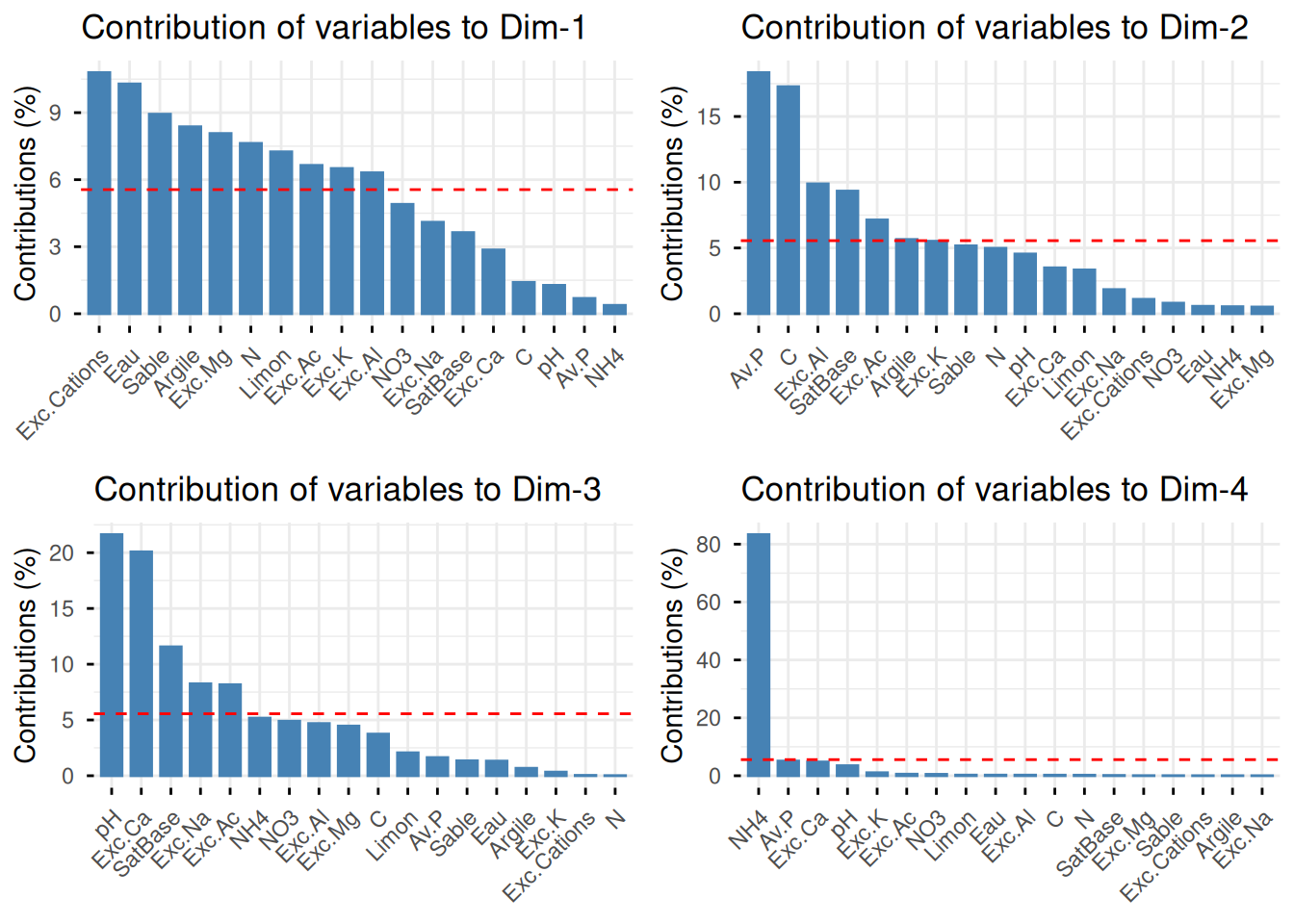
A l’aide des contributions des différentes variables à la définition des axes, on peut comprendre l’information résumée par ces axes.

Code 
dta_pca$var$contrib |> as.data.frame() |> arrange(-Dim.1) |> select(Dim.1)
                 Dim.1
Exc.Cations 10.7948976
Eau         10.2869537
Sable        8.9320337
Argile       8.3692915
Exc.Mg       8.0680012
N            7.6257192
Limon        7.2482479
Exc.Ac       6.6410790
Exc.K        6.5019985
Exc.Al       6.3103633
NO3          4.8972792
Exc.Na       4.0962613
SatBase      3.6327958
Exc.Ca       2.8569555
C            1.4042632
pH           1.2715181
Av.P         0.6866580
NH4          0.3756832
Code 
dta_pca$var$contrib |> as.data.frame() |> arrange(-Dim.2)|> select(Dim.2)
                 Dim.2
Av.P        18.3416002
C           17.2698714
Exc.Al       9.8791351
SatBase      9.3284152
Exc.Ac       7.1350777
Argile       5.6487034
Exc.K        5.5144861
Sable        5.1690662
N            4.9797246
pH           4.5458035
Exc.Ca       3.4929128
Limon        3.3331633
Exc.Na       1.8388125
Exc.Cations  1.0983771
NO3          0.8067869
Eau          0.5672494
NH4          0.5379330
Exc.Mg       0.5128816
Code 
dta_pca$var$contrib |> as.data.frame() |> arrange(-Dim.4) |> select(Dim.4)
                  Dim.4
NH4         83.32422550
Av.P         5.07745293
Exc.Ca       4.76531991
pH           3.47674191
Exc.K        1.04204242
Exc.Ac       0.54618975
NO3          0.49368347
Limon        0.22554066
Eau          0.22252392
Exc.Al       0.22067882
C            0.20730224
N            0.19798282
SatBase      0.10528835
Exc.Mg       0.03464235
Sable        0.02775744
Exc.Cations  0.01430037
Argile       0.01058951
Exc.Na       0.00773764

La description des axes

  • l’axe 1 parle de l’eau, des cations, du sable et de l’argile (et du limon)
  • l’axe 2 du phosphate et du carbone
  • petite remarque sur l’axe 4 qui est essentiellemnt NH4

On peut aussi utiliser uune visualisation plus graphique en utilisant factoextra

contri var axe 1

Code 
contrib_axe1 <- fviz_contrib(dta_pca, choice = 'var', axes = 1)
contrib_axe2 <- fviz_contrib(dta_pca, choice = 'var', axes = 2)
contrib_axe3 <- fviz_contrib(dta_pca, choice = 'var', axes = 3)
contrib_axe4 <- fviz_contrib(dta_pca, choice = 'var', axes = 4)
if("ggpubr" %in% installed.packages()[,1]){
  ggpubr::ggarrange( contrib_axe1, 
                     contrib_axe2, 
                     contrib_axe3,  
                     contrib_axe4,
                     ncol = 2, nrow = 2)
}

Individus

Pour représenter la projection des individus dans un plan principal, on utilise la fonction fviz_pca_ind.

Code 
# Représentation dans le premier plan_principal
fviz_pca_ind(dta_pca,
             axes = c(1, 2)) # Numéro des axes à représenter

Visualiser la profondeur sur les différents plans

  • Dans la fonction fviz_pca_ind, en rajoutant col.ind = donnees_sols$Sol, coloriez les individus selon leur profondeur.
Code 
# # Représentation dans le premier plan_principal
fviz_pca_ind(dta_pca,
              axes = c(1, 2),
              habillage=3)

visualiser les types de sol

  • Dans la fonction fviz_pca_ind, en rajoutant col.ind = donnees_sols$Sol, coloriez les individus selon leur type de sol.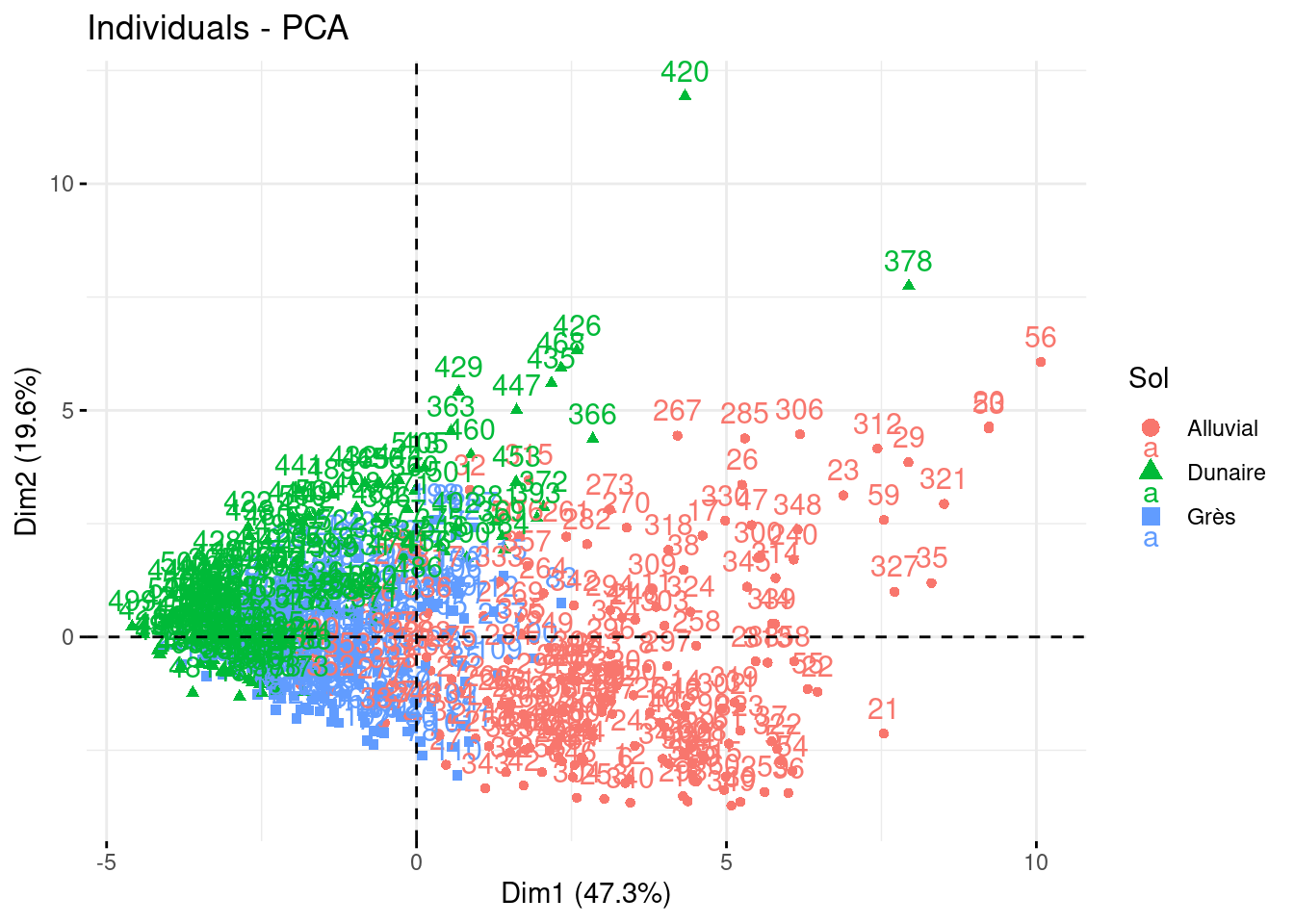
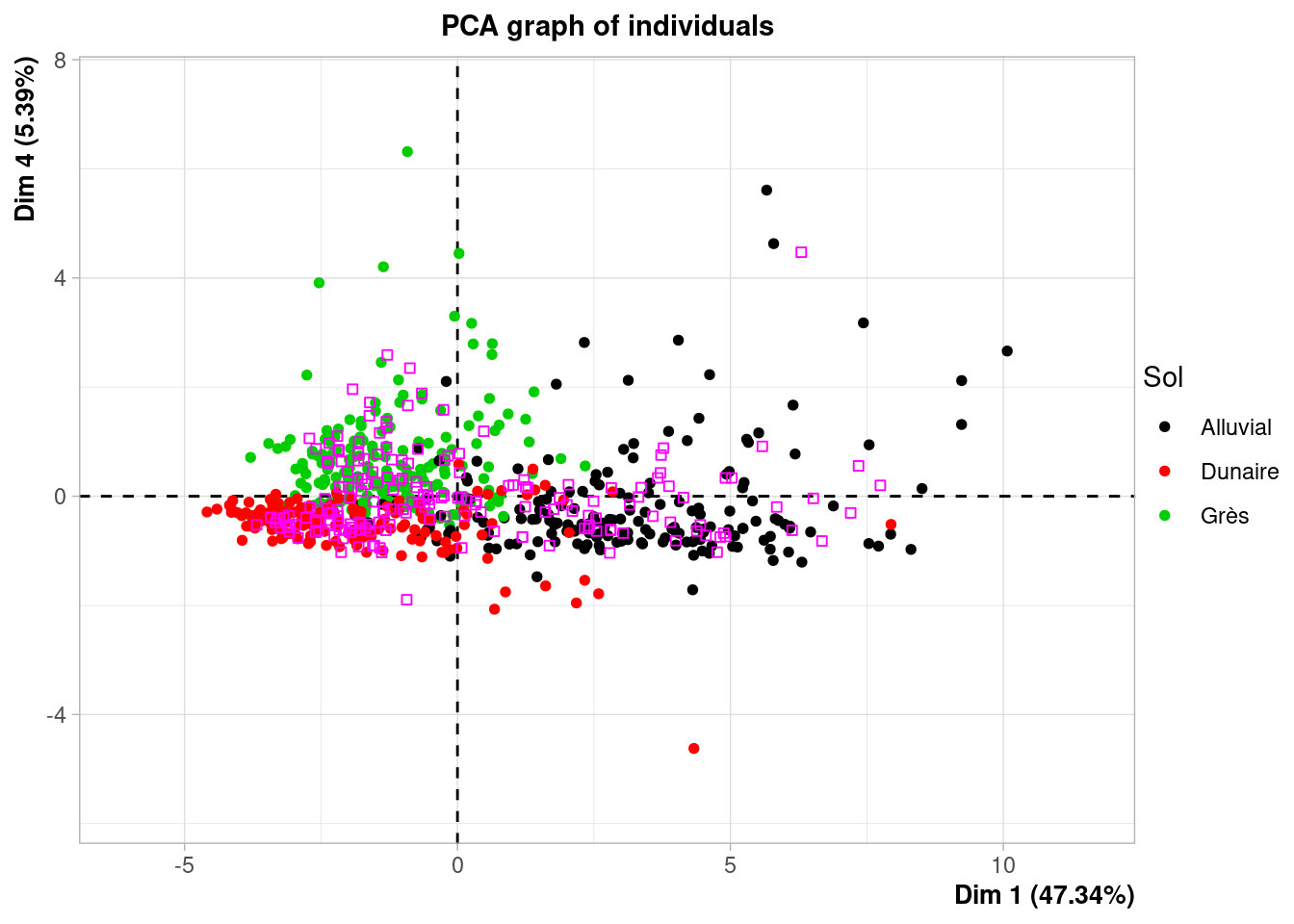
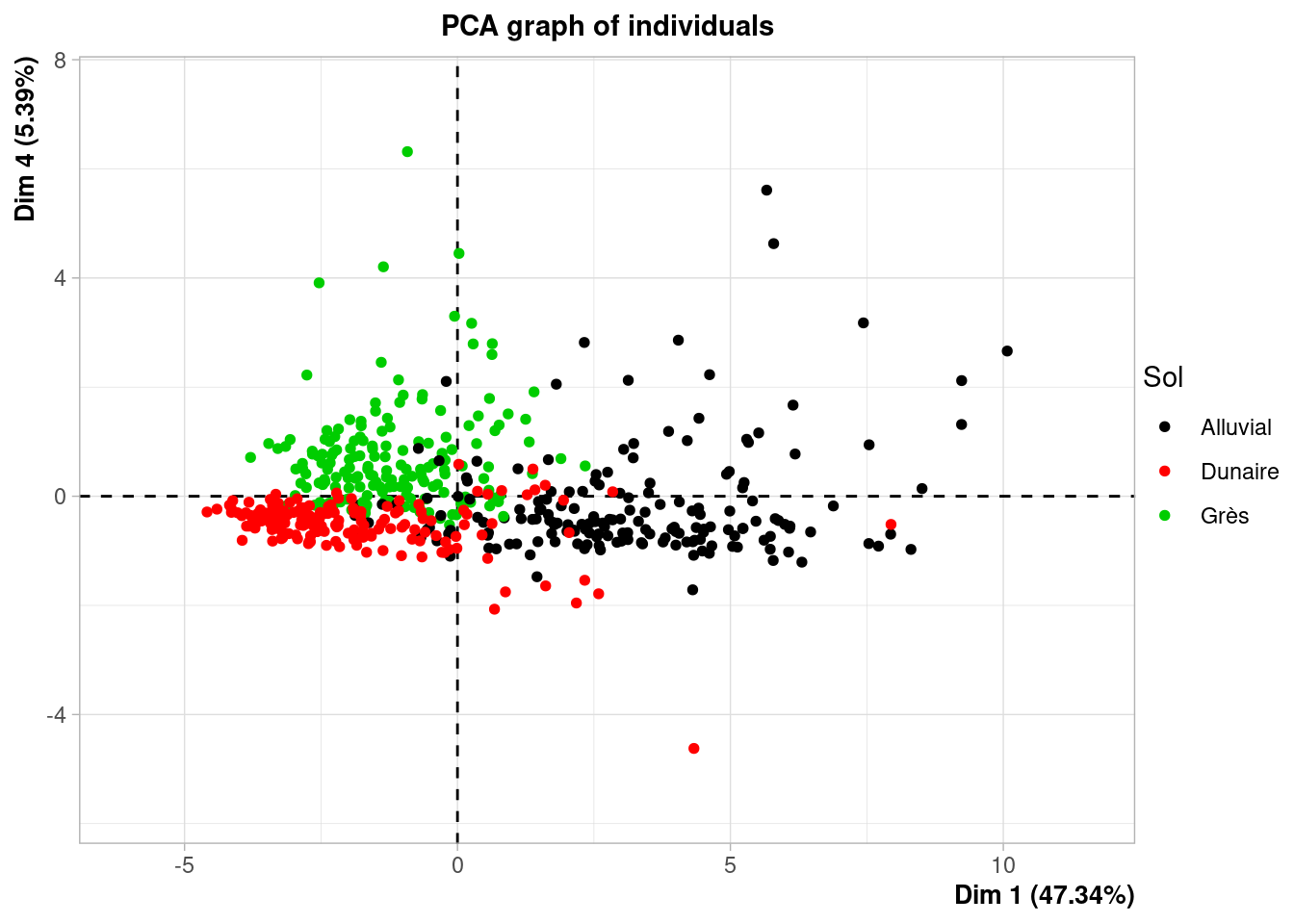
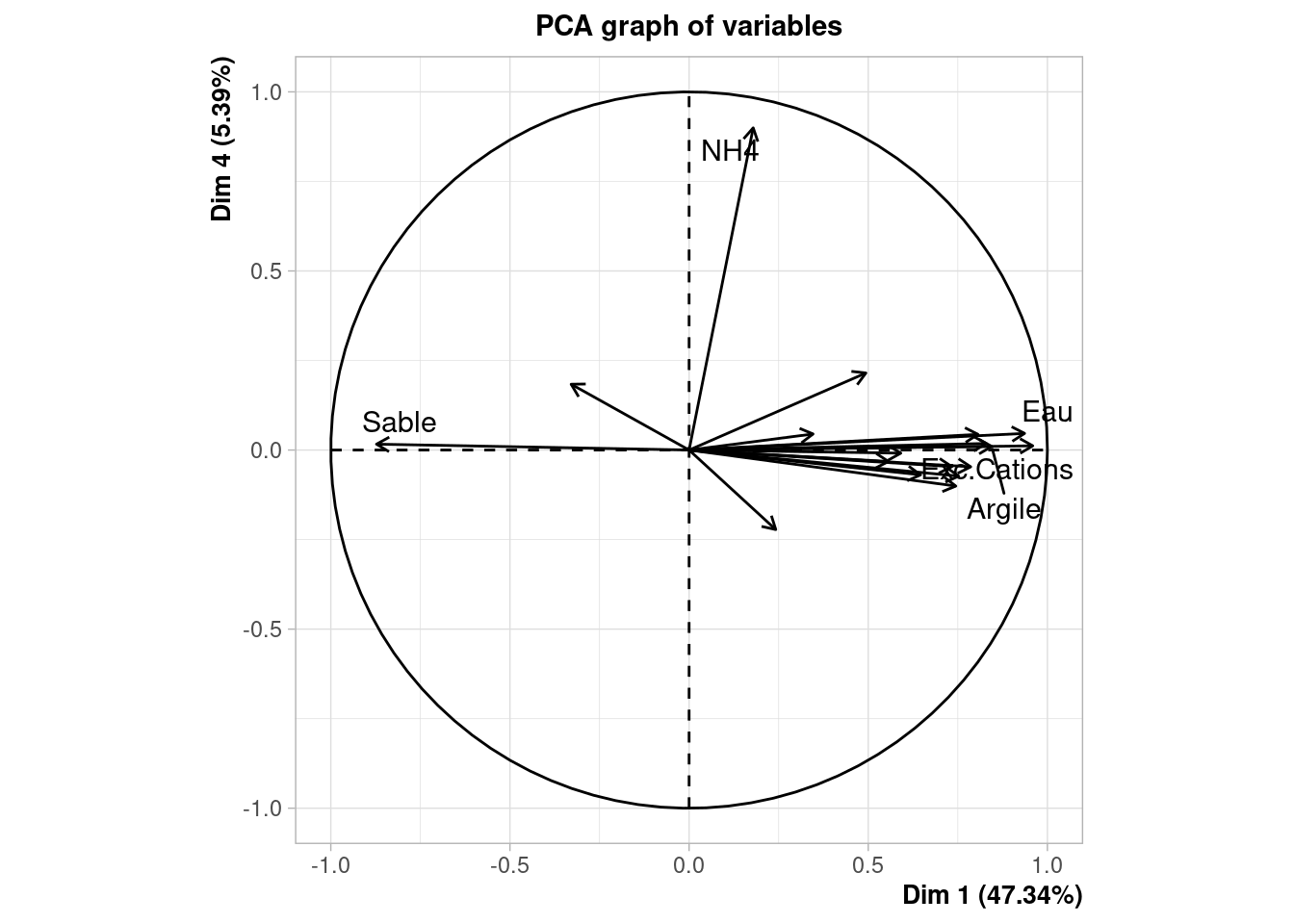
Code 
# # Représentation dans le premier plan_principal
fviz_pca_ind(dta_pca,
              axes = c(1, 2),
              habillage=1)

Code 
# Représentation dans le premier plan_principal
plot.PCA(dta_pca, 
         axes = c(1,4), invisible=c('ind.sup'),
         habillage=1, ## numero de la variable quali  à utiliser pour l'habillage
         label ='none')

Code 
plot.PCA(dta_pca, axes=c(1,4),invisible=c('quali','ind.sup'),habillage=1,label ='none')

Code 
plot.PCA(dta_pca,choix='var',
         select='cos2  0.7', ## pour représenter seulement les variables dont le cos2 > 0.7
         unselect=0, axes = c(1,4) )

il fallait chercher l’axe 4 pour bien illustrer les différences entre grès et dunaire, l’axe 4 est presque exclusivement l’information sur le NH4.